+ - 0:00:00
Notes for current slide
Notes for next slide

2.1 — Data 101 & Descriptive Statistics

ECON 480 • Econometrics • Fall 2020

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsF20
metricsF20.classes.ryansafner.com

Outline

The Two Big Problems with Data

Data 101

Descriptive Statistics

Measures of Center

Measures of Dispersion

The Two Big Problems with Data

Two Big Problems with Data

  • We want to use econometrics to identify causal relationships and make inferences about them

  1. Problem for identification: endogeneity

  2. Problem for inference: randomness

Identification Problem: Endogeneity

  • An independent variable (X) is exogenous if its variation is unrelated to other factors that affect the dependent variable (Y)

  • An independent variable (X) is endogenous if its variation is related to other factors that affect the dependent variable (Y)

Identification Problem: Endogeneity

  • An independent variable (X) is exogenous if its variation is unrelated to other factors that affect the dependent variable (Y)

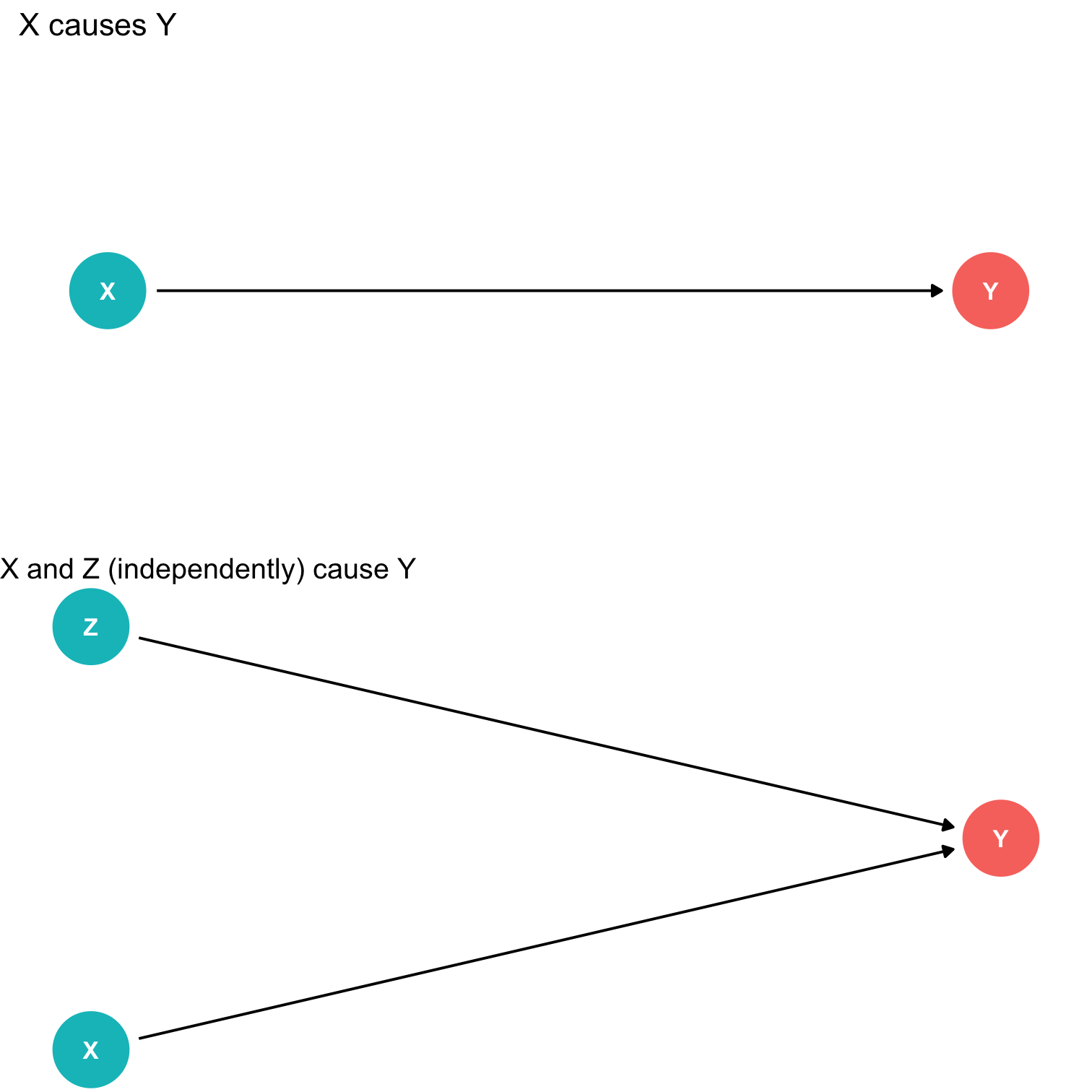
Identification Problem: Endogeneity

  • An independent variable (X) is endogenous if its variation is related to other factors that affect the dependent variable (Y)

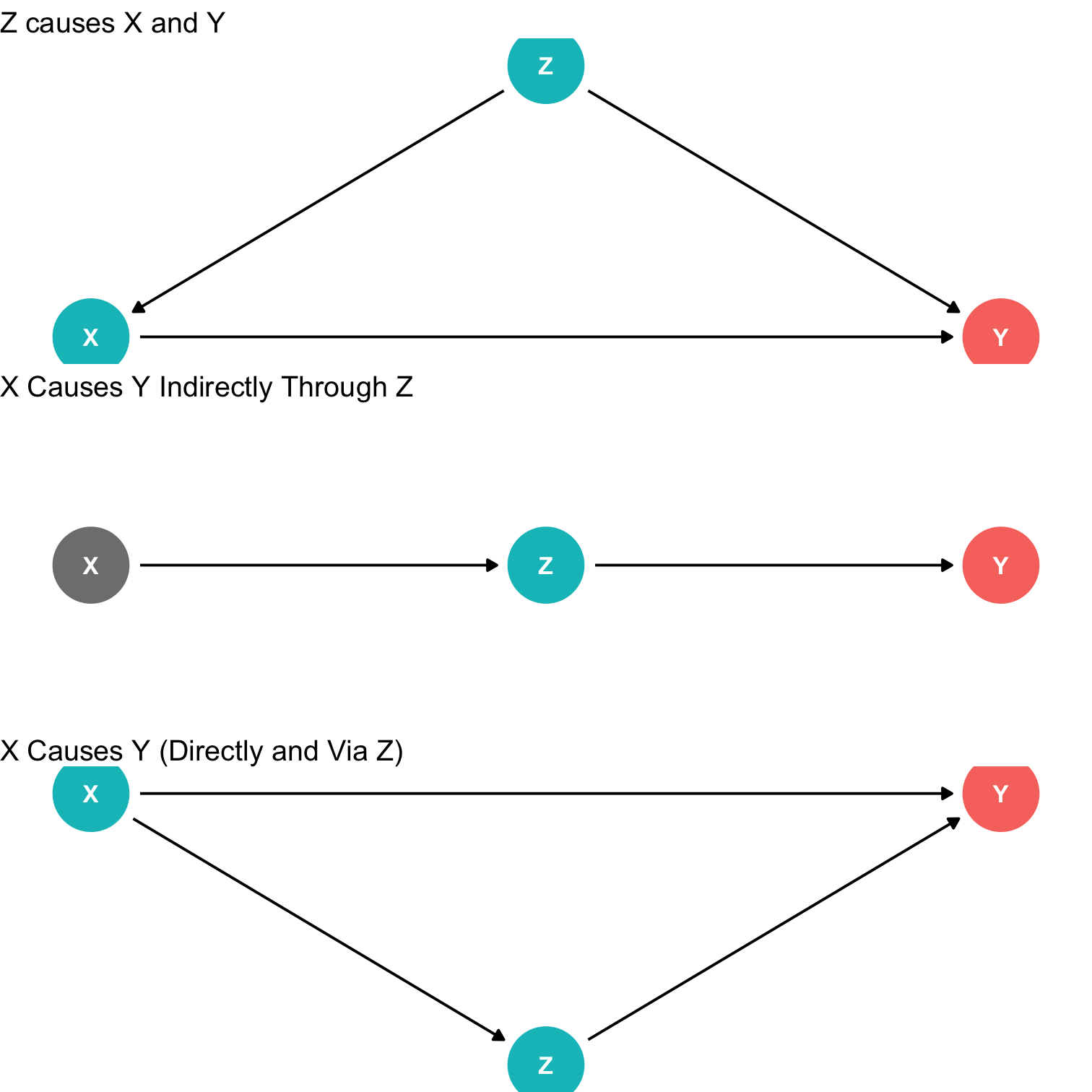
Inference Problem: Randomness

  • Data is random due to natural sampling variation
    • Taking one sample of a population will yield slightly different information than another sample of the same population

  • Common in statistics, easy to fix

  • Inferential Statistics: making claims about a wider population using sample data

    • We use common tools and techniques to deal with randomness

The Two Problems: Where We're Heading...Ultimately

Sample →⏟statistical inference Population →⏟causal indentification Unobserved Parameters

  • We want to identify causal relationships between population variables

    • Logically first thing to consider
    • Endogeneity problem

  • We'll use sample statistics to infer something about population parameters

    • In practice, we'll only ever have a finite sample distribution of data
    • We don't know the population distribution of data
    • Randomness problem

Data 101

Data 101

  • Data are information with context

  • Individuals are the entities described by a set of data

    • e.g. persons, households, firms, countries

Data 101

  • Variables are particular characteristics about an individual

    • e.g. age, income, profits, population, GDP, marital status, type of legal institutions

  • Observations or cases are the separate individuals described by a collection of variables

    • e.g. for one individual, we have their age, sex, income, education, etc.

  • individuals and observations are not necessarily the same:

    • e.g. we can have multiple observations on the same individual over time

Categorical Data

  • Categorical data place an individual into one of several possible categories

    • e.g. sex, season, political party
    • may be responses to survey questions
    • can be quantitative (e.g. age, zip code)

  • In R: character or factor type data

    • factor ⟹ specific possible categories

Categorical Data: Visualizing I

diamonds %>%
  count(cut) %>%
  mutate(frequency = n / sum(n),
         percent = round(frequency * 100, 2))
Summary of diamonds by cut
cut n frequency percent
Fair 1610 0.0298480 2.98
Good 4906 0.0909529 9.10
Very Good 12082 0.2239896 22.40
Premium 13791 0.2556730 25.57
Ideal 21551 0.3995365 39.95

  • Good way to represent categorical data is with a frequency table

  • Count (n): total number of individuals in a category

  • Frequency: proportion of a category's ocurrence relative to all data

    • Multiply proportions by 100% to get percentages

Categorical Data: Visualizing II

  • Charts and graphs are always better ways to visualize data

  • A bar graph represents categories as bars, with lengths proportional to the count or relative frequency of each category

ggplot(diamonds, aes(x=cut,
                     fill=cut))+
  geom_bar()+
  guides(fill=F)+
  theme_pander(base_family = "Fira Sans Condensed",
           base_size=20)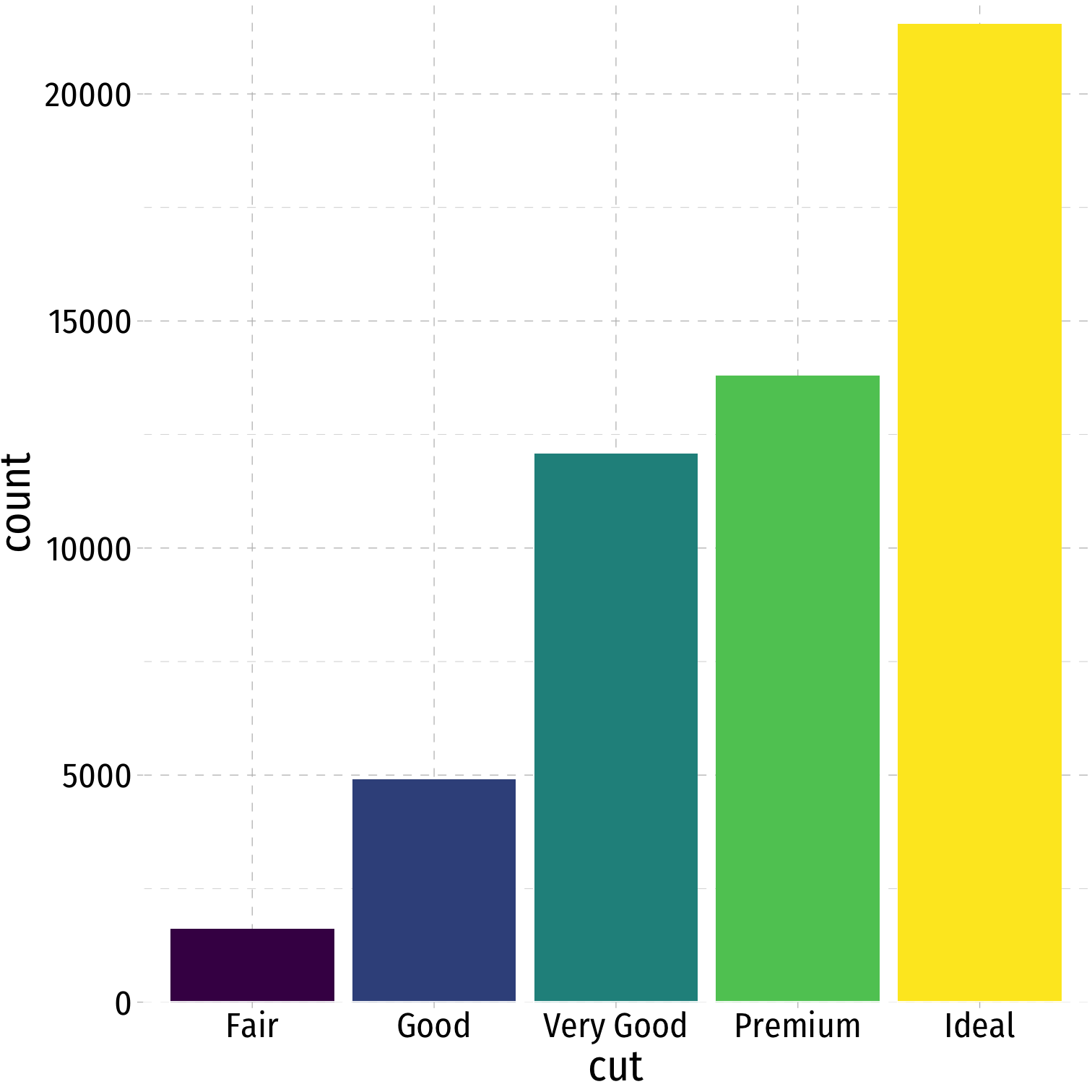

Categorical Data: Visualizing III

  • Avoid pie charts!

  • People are not good at judging 2-d differences (angles, area)

  • People are good at judging 1-d differences (length)

Categorical Data: Visualizing III

  • Avoid pie charts!

  • People are not good at judging 2-d differences (angles, area)

  • People are good at judging 1-d differences (length)

Categorical Data: Visualizing IV

  • Maybe a stacked bar chart
diamonds %>%
  count(cut) %>%
ggplot(data = .)+
  aes(x = "",
      y = n)+
  geom_col(aes(fill = cut))+
  geom_label(aes(label = cut,
                 color = cut),
             position = position_stack(vjust = 0.5)
             )+
  guides(color = F,
         fill = F)+
  theme_void()

Categorical Data: Visualizing IV

  • Maybe lollipop chart
diamonds %>%
  count(cut) %>%
  mutate(cut_name = as.factor(cut)) %>%
ggplot(., aes(x = cut_name, y = n, color = cut))+
 geom_point(stat="identity",
            fill="black",
            size=12)  +
  geom_segment(aes(x = cut_name, y = 0,
                   xend = cut_name,
                   yend = n), size = 2)+
  geom_text(aes(label = n),color="white", size=3) +
  coord_flip()+
  labs(x = "Cut")+
  theme_pander(base_family = "Fira Sans Condensed",
                base_size=20)+
  guides(color = F)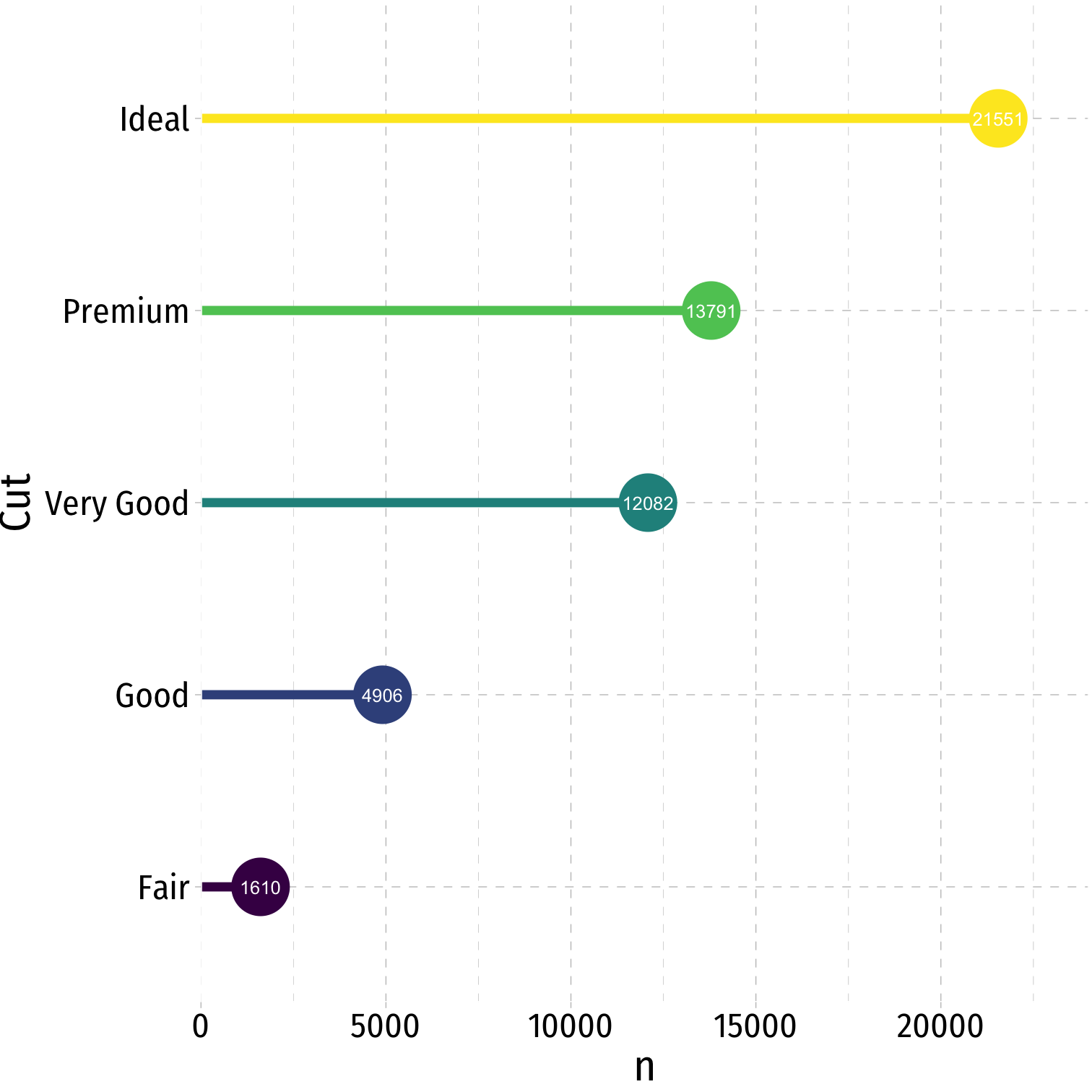

Categorical Data: Visualizing IV

  • Maybe a treemap
library(treemapify)
diamonds %>%
  count(cut) %>%
ggplot(., aes(area = n, fill = cut)) +
  geom_treemap() +
  guides(fill = FALSE) +
  geom_treemap_text(aes(label = cut),
                    colour = "white",
                    place = "topleft",
                    grow = TRUE)

Quantitative Data I

  • Quantitative variables take on numerical values of equal units that describe an individual

    • Units: points, dollars, inches
    • Context: GPA, prices, height

  • We can mathematically manipulate only quantitative data

    • e.g. sum, average, standard deviation

  • In R: numeric type data

    • integer if whole number
    • double if has decimals

Discrete Data

  • Discrete data are finite, with a countable number of alternatives

  • Categorical: place data into categories

    • e.g. letter grades: A, B, C, D, F
    • e.g. class level: freshman, sophomore, junior, senior

  • Quantitative: integers

    • e.g. SAT Score, number of children, age (years)

Continuous Data

  • Continuous data are infinitely divisible, with an uncountable number of alternatives

    • e.g. weight, length, temperature, GPA

  • Many discrete variables may be treated as if they are continuous

    • e.g. SAT scores (whole points), wages (dollars and cents)

Spreadsheets

ID Name Age Sex Income
1 John 23 Male 41000
2 Emile 18 Male 52600
3 Natalya 28 Female 48000
4 Lakisha 31 Female 60200
5 Cheng 36 Male 81900

  • The most common data structure we use is a spreadsheet

    • In R: a data.frame or tibble

  • A row contains data about all variables for a single individual

  • A column contains data about a single variable across all individuals

Spreadsheets

ID Name Age Sex Income
1 John 23 Male 41000
2 Emile 18 Male 52600
3 Natalya 28 Female 48000
4 Lakisha 31 Female 60200
5 Cheng 36 Male 81900
  • Each cell can be referenced by its row and column (in that order!), df[row,column]
example[3,2] # value in row 3, column 2
## # A tibble: 1 x 1
##   Name   
##   <chr>  
## 1 Natalya

Spreadsheets II

  • It is common to use some notation like the following:

  • Let {x1,x2,⋯,xn} be a simple data series on variable X

    • n individual observations
    • xi is the value of the ith observation for i=1,2,⋯,n

Spreadsheets II

  • It is common to use some notation like the following:

  • Let {x1,x2,⋯,xn} be a simple data series on variable X

    • n individual observations
    • xi is the value of the ith observation for i=1,2,⋯,n

Quick Check: Let x represent the score on a homework assignment: 75,100,92,87,79,0,95

  1. What is n?
  2. What is x1?
  3. What is x6?

Datasets: Cross-Sectional

ID Name Age Sex Income
1 John 23 Male 41000
2 Emile 18 Male 52600
3 Natalya 28 Female 48000
4 Lakisha 31 Female 60200
5 Cheng 36 Male 81900

  • Cross-sectional data: observations of individuals at a given point in time

  • Each observation is a unique individual xi

  • Simplest and most common data

  • A "snapshot" to compare differences across individuals

Datasets: Time-Series

Year GDP Unemployment CPI
1950 8.2 0.06 100
1960 9.9 0.04 118
1970 10.2 0.08 130
1980 12.4 0.08 190
1985 13.6 0.06 196

  • Time-series data: observations of the same individual(s) over time

  • Each observation is a time period xt

  • Often used for macroeconomics, finance, and forecasting

  • Unique challenges for time series

  • A "moving picture" to see how individuals change over time

Datasets: Panel

City Year Murders Population UR
Philadelphia 1986 5 3.700 8.7
Philadelphia 1990 8 4.200 7.2
D.C. 1986 2 0.250 5.4
D.C. 1990 10 0.275 5.5
New York 1986 3 6.400 9.6

  • Panel, or longitudinal dataset: a time-series for each cross-sectional entity

    • Must be same individuals over time

  • Each obs. is an individual in a time period xit

  • More common today for serious researchers; unique challenges and benefits

  • A combination of "snapshot" comparisons over time

Descriptive Statistics

Variables and Distributions

  • Variables take on different values, we can describe a variable's distribution (of these values)

  • We want to visualize and analyze distributions to search for meaningful patterns using statistics

Two Branches of Statistics

  • Two main branches of statistics:

  1. Descriptive Statistics: describes or summarizes the properties of a sample

  2. Inferential Statistics: infers properties about a larger population from the properties of a sample†

† We'll encounter inferential statistics mainly in the context of regression later.

Histograms

  • A common way to present a quantitative variable's distribution is a histogram

    • The quantitative analog to the bar graph for a categorical variable

  • Divide up values into bins of a certain size, and count the number of values falling within each bin, representing them visually as bars

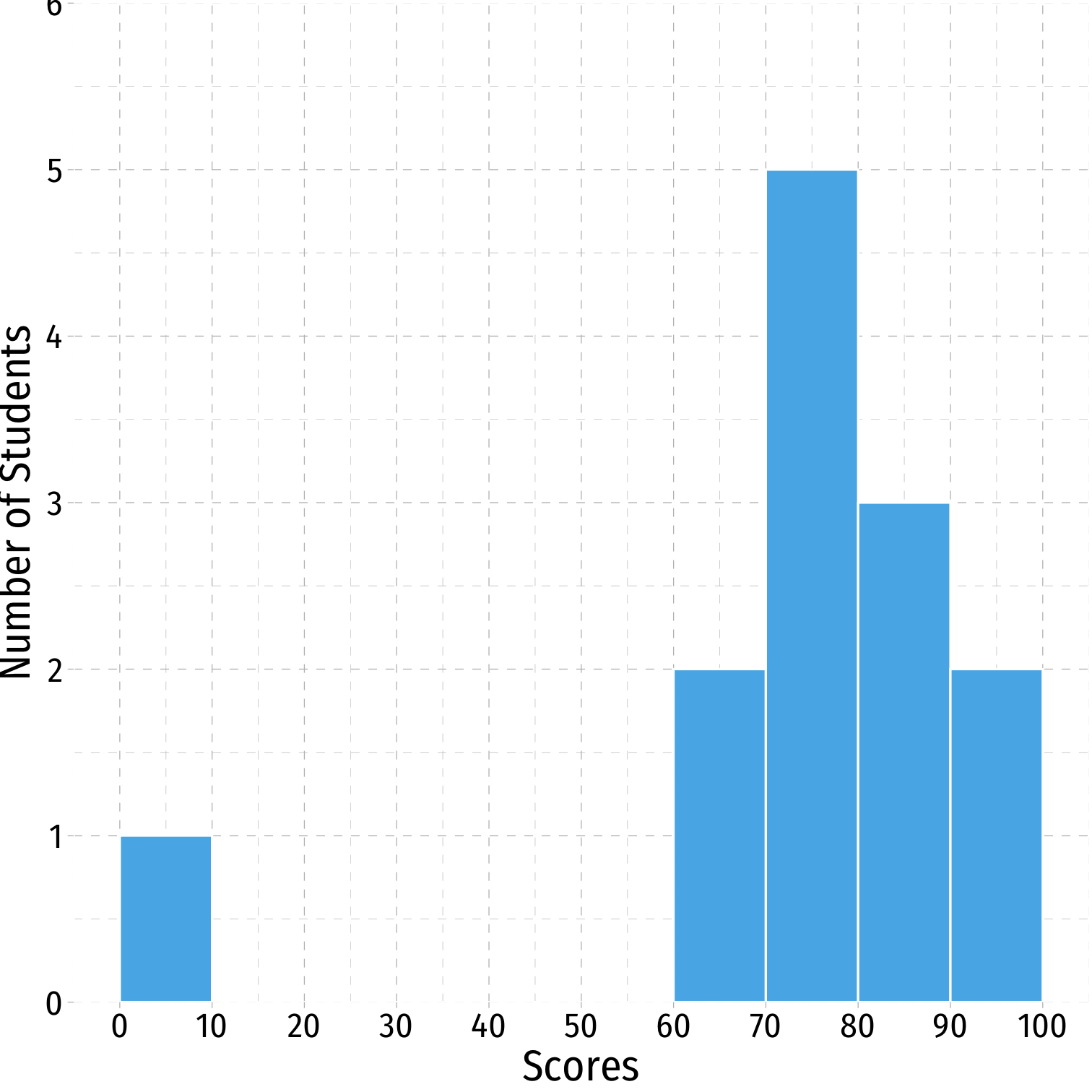
Histogram: Example

Example: a class of 13 students takes a quiz (out of 100 points) with the following results:

{0,62,66,71,71,74,76,79,83,86,88,93,95}

Histogram: Example

Example: a class of 13 students takes a quiz (out of 100 points) with the following results:

{0,62,66,71,71,74,76,79,83,86,88,93,95}

quizzes<-tibble(scores = c(0,62,66,71,71,74,76,79,83,86,88,93,95))

Histogram: Example

Example: a class of 13 students takes a quiz (out of 100 points) with the following results:

{0,62,66,71,71,74,76,79,83,86,88,93,95}

h<-ggplot(quizzes,aes(x=scores))+
  geom_histogram(breaks = seq(0,100,10),
                 color = "white",
                 fill = "#56B4E9")+
  scale_x_continuous(breaks = seq(0,100,10))+
  scale_y_continuous(limits = c(0,6), expand = c(0,0))+
  labs(x = "Scores",
       y = "Number of Students")+
  ggthemes::theme_pander(base_family = "Fira Sans Condensed",
           base_size=20)
h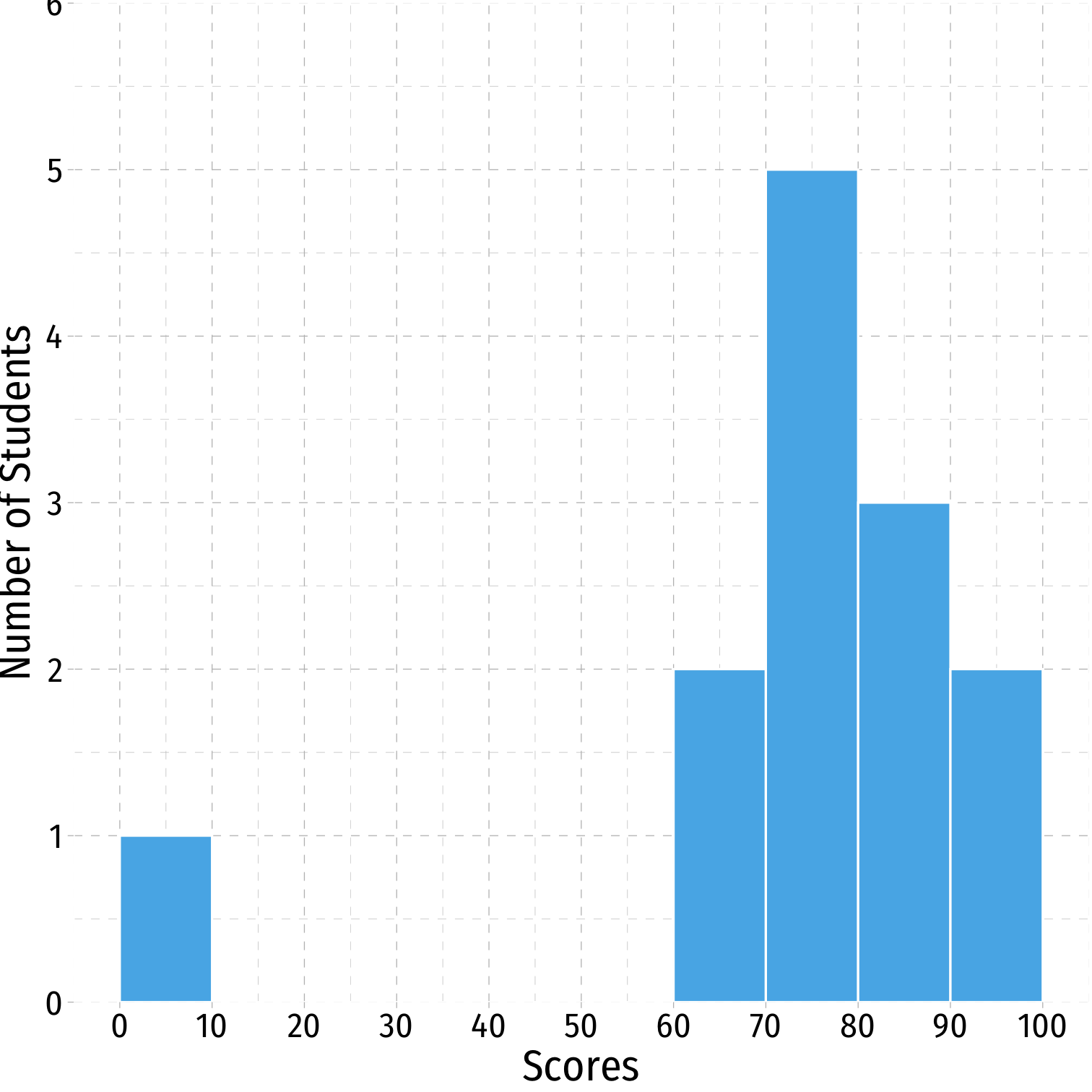

Descriptive Statistics

  • We are often interested in the shape or pattern of a distribution, particularly:
    • Measures of center
    • Measures of dispersion
    • Shape of distribution

Measures of Center

Mode

  • The mode of a variable is simply its most frequent value

  • A variable can have multiple modes

Mode

  • The mode of a variable is simply its most frequent value

  • A variable can have multiple modes

Example: a class of 13 students takes a quiz (out of 100 points) with the following results:

{0,62,66,71,71,74,76,79,83,86,88,93,95}

Mode

  • There is no dedicated mode() function in R, surprisingly

  • A workaround in dplyr: 

quizzes %>%
  count(scores) %>%
  arrange(desc(n))
## # A tibble: 12 x 2
##    scores     n
##     <dbl> <int>
##  1     71     2
##  2      0     1
##  3     62     1
##  4     66     1
##  5     74     1
##  6     76     1
##  7     79     1
##  8     83     1
##  9     86     1
## 10     88     1
## 11     93     1
## 12     95     1

Multi-Modal Distributions

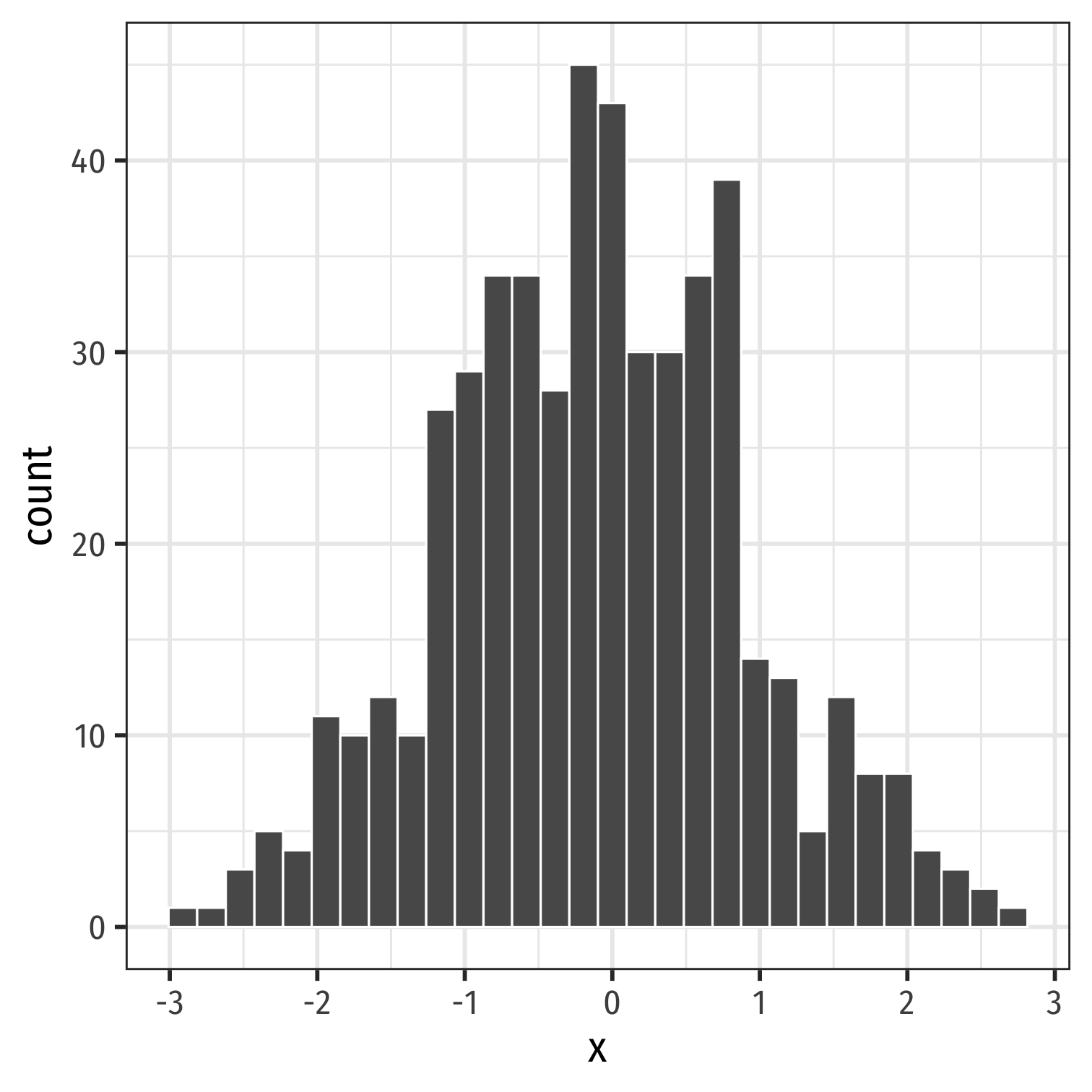
  • Looking at a histogram, the modes are the "peaks" of the distribution

    • Note: depends on how wide you make the bins!

  • May be unimodal, bimodal, trimodal, etc

Symmetry and Skew I

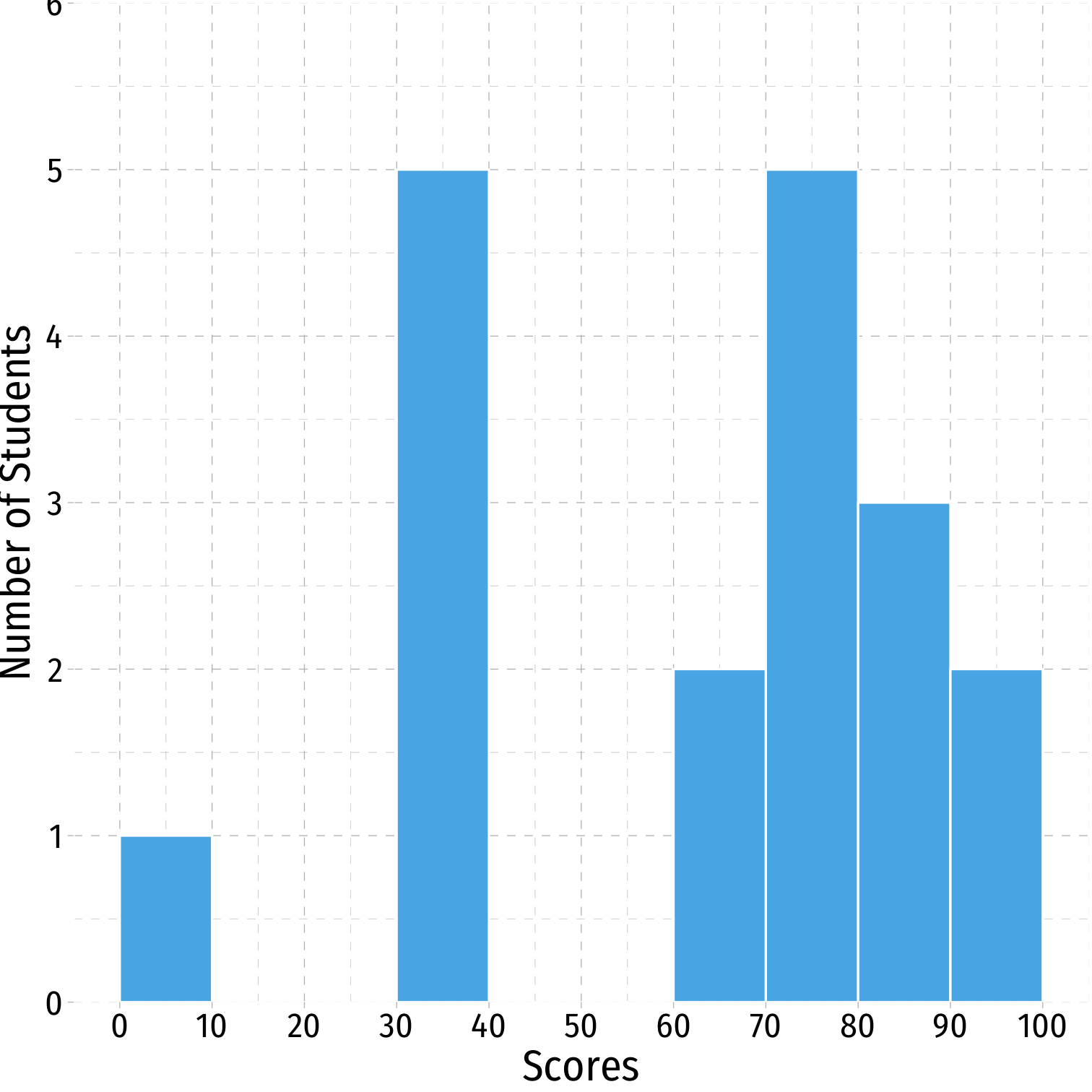
  • A distribution is symmetric if it looks roughly the same on either side of the "center"

  • The thinner ends (far left and far right) are called the tails of a distribution

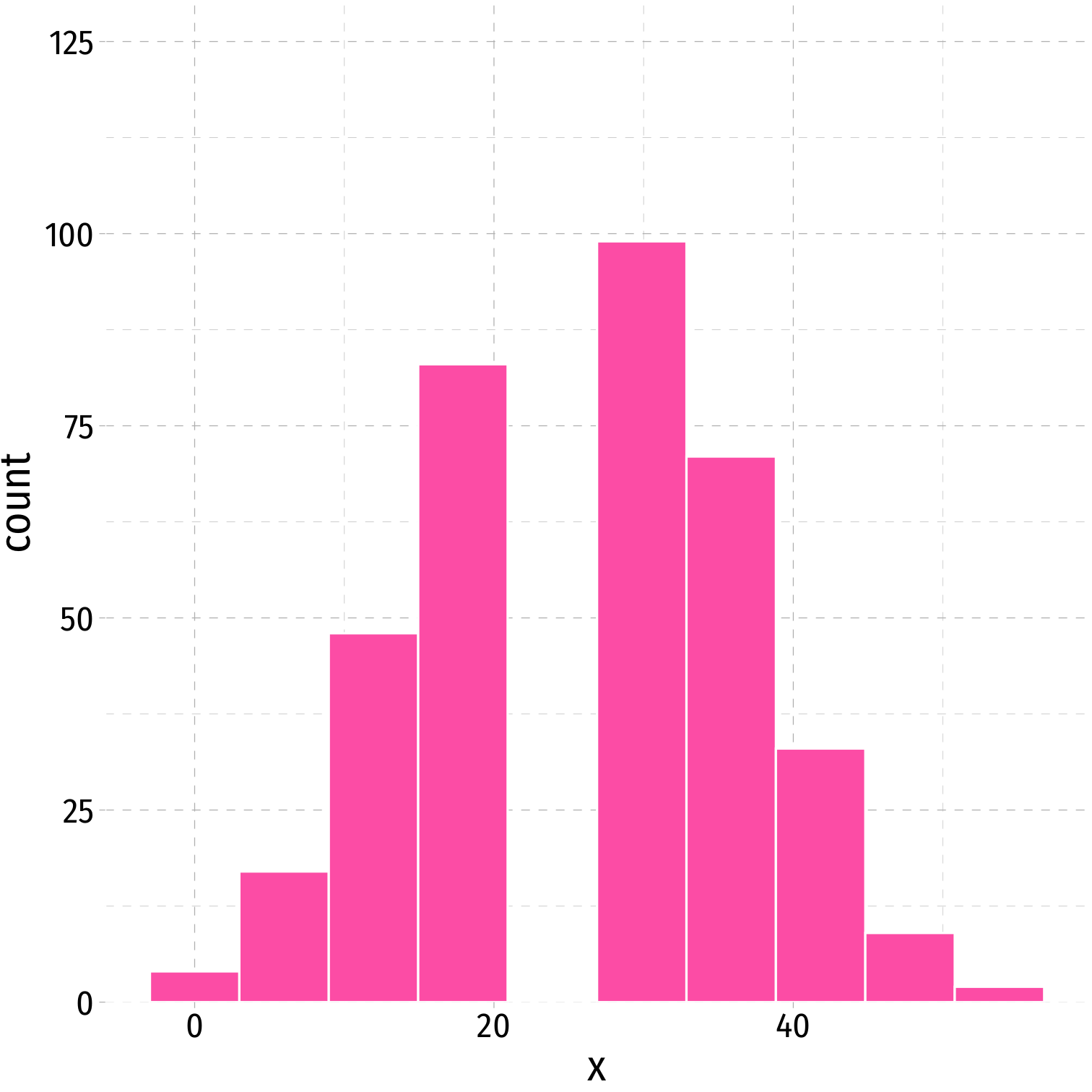
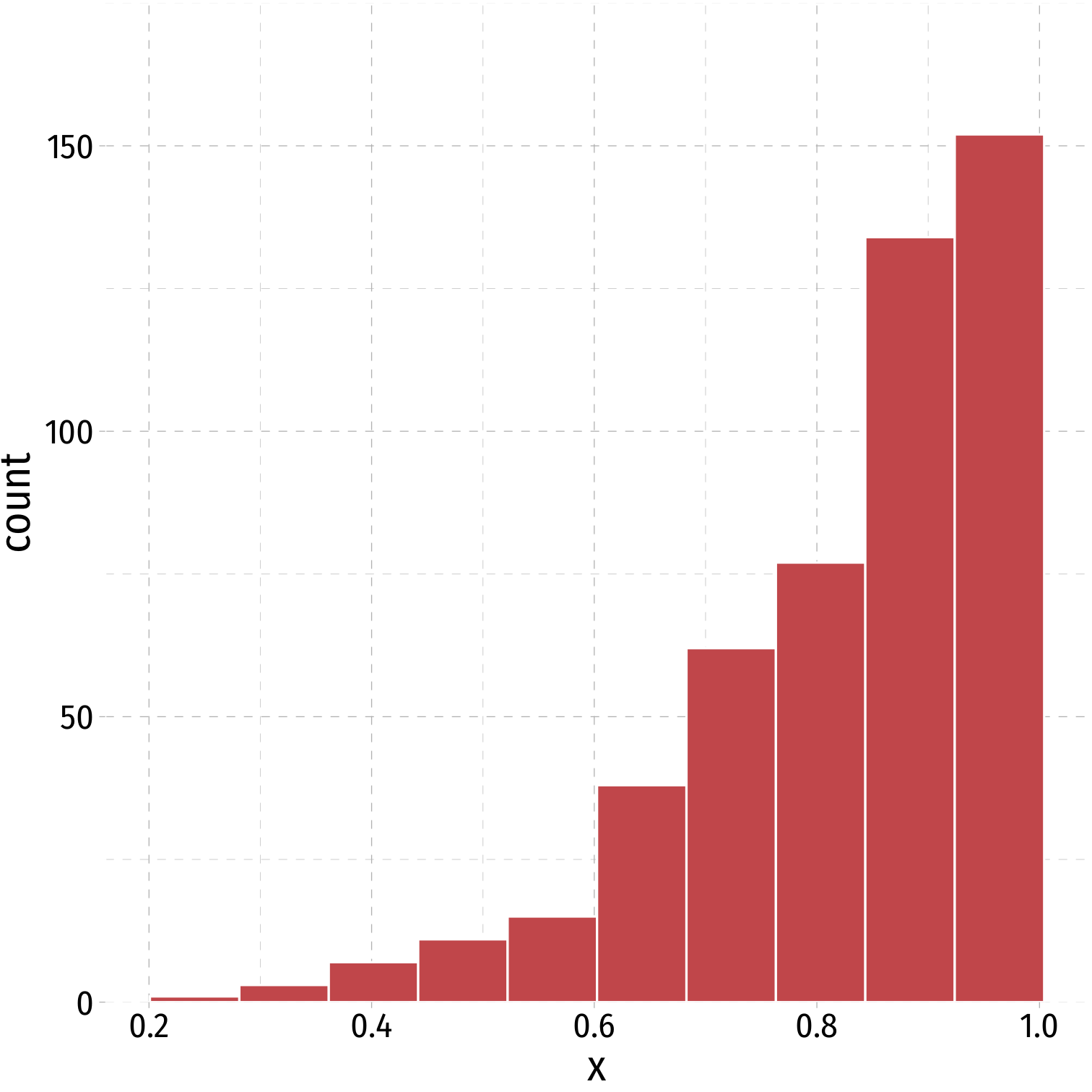
Symmetry and Skew I

  • If one tail stretches farther than the other, distribution is skewed in the direction of the longer tail

Outliers

  • Outlier: extreme value that does not appear part of the general pattern of a distribution

  • Can strongly affect descriptive statistics

  • Might be the most informative part of the data

  • Could be the result of errors

  • Should always be explored and discussed!

Arithmetic Mean (Population)

  • The natural measure of the center of a population's distribution is its "average" or arithmetic mean (μ)

μ=x1+x2+...+xNN=1NN∑i=1xi

  • For N values of variable x, "mu" is the sum of all individual x values (xi) from 1 to N, divided by the N number of values†

  • See today's class notes for more about the summation operator, Σ, it'll come up again!

† Note the mean need not be an actual value of the data!

Arithmetic Mean (Sample)

  • When we have a sample, we compute the sample mean (ˉx)

ˉx=x1+x2+...+xnn=1nn∑i=1xi

  • For n values of variable x, "x-bar" is the sum of all individual x values (xi) divided by the n number of values

Arithmetic Mean (Sample)

  • When we have a sample, we compute the sample mean (ˉx)

ˉx=x1+x2+...+xnn=1nn∑i=1xi

  • For n values of variable x, "x-bar" is the sum of all individual x values (xi) divided by the n number of values

Example:

{0,62,66,71,71,74,76,79,83,86,88,93,95}

ˉx=113(0+62+66+71+71+74+76+79+83+86+88+93+95)ˉx=94413ˉx=72.62

Arithmetic Mean (Sample)

  • When we have a sample, we compute the sample mean (ˉx)

ˉx=x1+x2+...+xnn=1nn∑i=1xi

  • For n values of variable x, "x-bar" is the sum of all individual x values (xi) divided by the n number of values

Example:

{0,62,66,71,71,74,76,79,83,86,88,93,95}

ˉx=113(0+62+66+71+71+74+76+79+83+86+88+93+95)ˉx=94413ˉx=72.62

quizzes %>%
  summarize(mean=mean(scores))
## # A tibble: 1 x 1
##    mean
##   <dbl>
## 1  72.6

Arithmetic Mean: Affected by Outliers

  • If we drop the outlier (0)

Arithmetic Mean: Affected by Outliers

  • If we drop the outlier (0)

Example:

{62,66,71,71,74,76,79,83,86,88,93,95}

ˉx=112(62+66+71+71+74+76+79+83+86+88+93+95)=94412=78.67

Arithmetic Mean: Affected by Outliers

  • If we drop the outlier (0)

Example:

{62,66,71,71,74,76,79,83,86,88,93,95}

ˉx=112(62+66+71+71+74+76+79+83+86+88+93+95)=94412=78.67

quizzes %>%
  filter(scores>0) %>%
  summarize(mean=mean(scores))
## # A tibble: 1 x 1
##    mean
##   <dbl>
## 1  78.7

Median

{0,62,66,71,71,74,76,79,83,86,88,93,95}

  • The median is the midpoint of the distribution

    • 50% to the left of the median, 50% to the right of the median

  • Arrange values in numerical order

    • For odd n: median is middle observation
    • For even n: median is average of two middle observations

Mean, Median, and Outliers

Mean, Median, Symmetry, Skew I

  • Symmetric distribution: mean ≈ median
symmetric %>%
  summarize(mean = mean(x),
            median = median(x))
## # A tibble: 1 x 2
##    mean median
##   <dbl>  <dbl>
## 1     4      4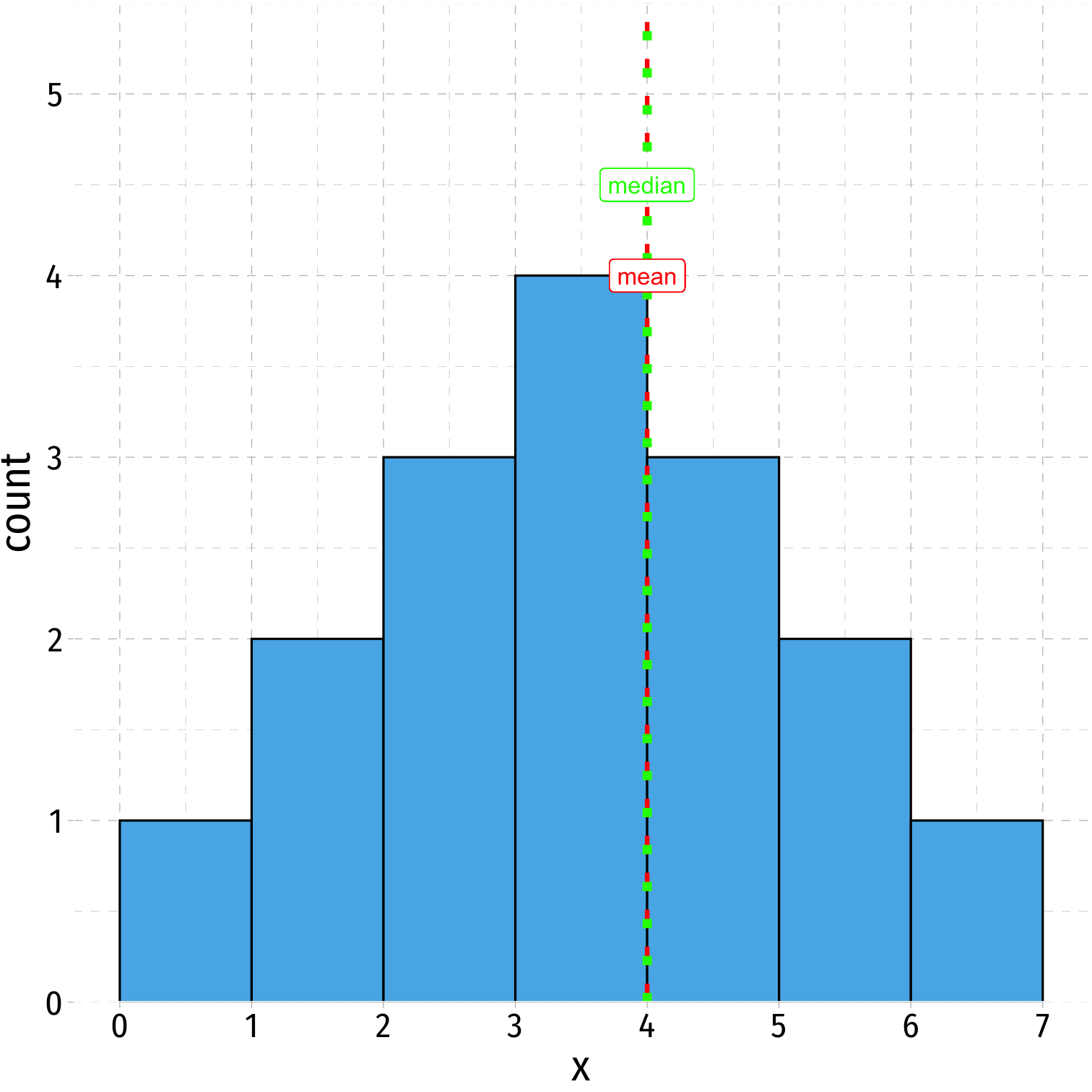

Mean, Median, Symmetry, Skew II

  • Left-skewed: mean < median
leftskew %>%
  summarize(mean = mean(x),
            median = median(x))
##       mean median
## 1 4.615385      5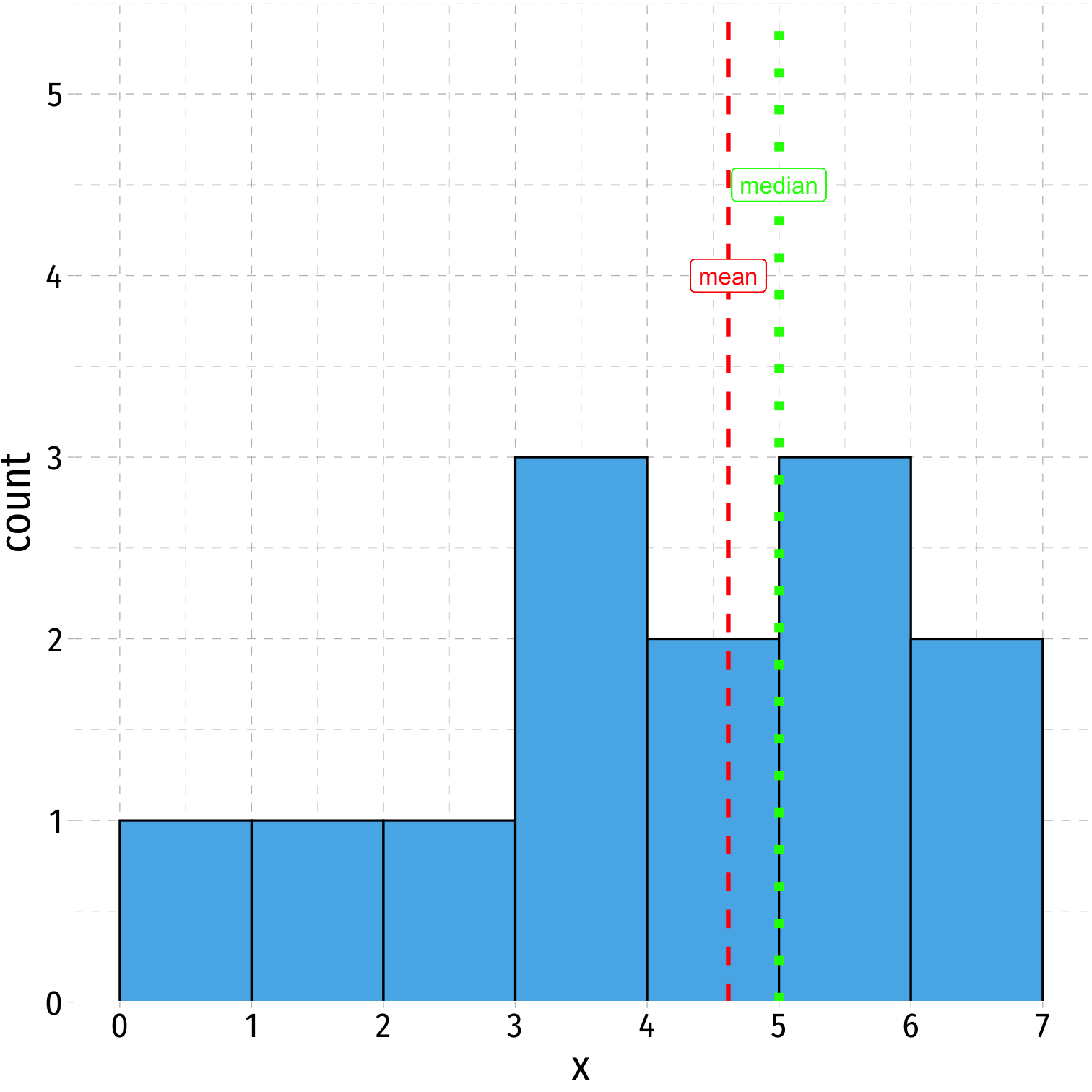

Mean, Median, Symmetry, Skew III

  • Right-skewed: mean > median
rightskew %>%
  summarize(mean = mean(x),
            median = median(x))
## # A tibble: 1 x 2
##    mean median
##   <dbl>  <dbl>
## 1  3.38      3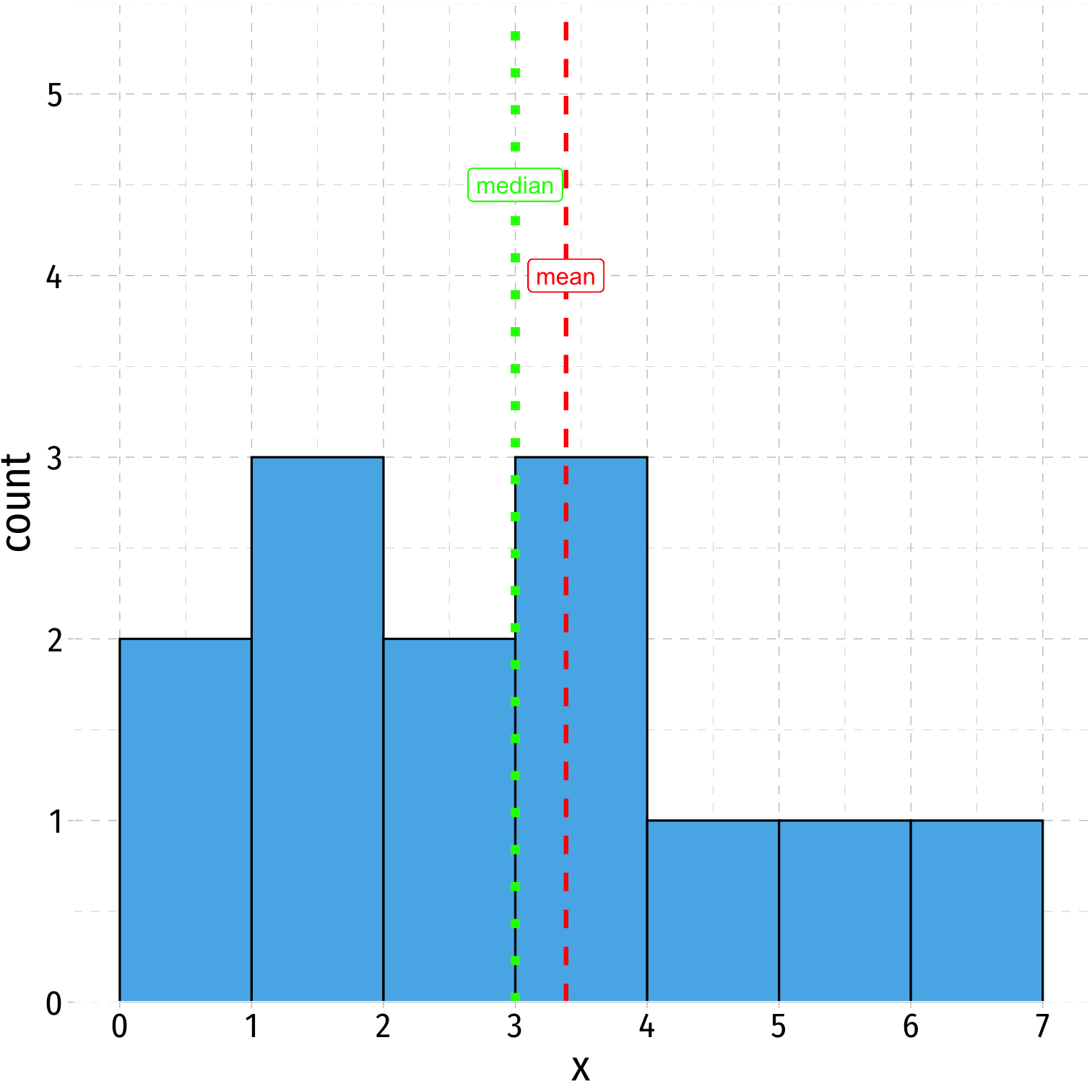

Measures of Dispersion

Measures of Dispersion: Range

  • The more variation in the data, the less helpful a measure of central tendency will tell us

  • Beyond just the center, we also want to measure the spread

  • Simplest metric is range =max−min

Measures of Dispersion: 5 Number Summary I

  • Common set of summary statistics of a distribution: "five number summary":
  1. Minimum value
  2. 25th percentile (Q1, median of first 50% of data)
  3. 50th percentile (median, Q2)
  4. 25th percentile (Q3, median of last 50% of data)
  5. Maximum value

Measures of Dispersion: 5 Number Summary I

  • Common set of summary statistics of a distribution: "five number summary":
  1. Minimum value
  2. 25th percentile (Q1, median of first 50% of data)
  3. 50th percentile (median, Q2)
  4. 25th percentile (Q3, median of last 50% of data)
  5. Maximum value
# Base R summary command (includes Mean)
summary(quizzes$scores)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    0.00   71.00   76.00   72.62   86.00   95.00
quizzes %>% # dplyr
  summarize(Min = min(scores),
            Q1 = quantile(scores, 0.25),
            Median = median(scores),
            Q3 = quantile(scores, 0.75),
            Max = max(scores))
## # A tibble: 1 x 5
##     Min    Q1 Median    Q3   Max
##   <dbl> <dbl>  <dbl> <dbl> <dbl>
## 1     0    71     76    86    95

Measures of Dispersion: 5 Number Summary II

  • The nth percentile of a distribution is the value that places n percent of values beneath it
quizzes %>%
  summarize("37th percentile" = quantile(scores,0.37))
## # A tibble: 1 x 1
##   `37th percentile`
##               <dbl>
## 1              72.3

Boxplots I

  • Boxplots are a great way to visualize the 5 number summary

  • Height of box: Q1 to Q3 (known as interquartile range (IQR), middle 50% of data)

  • Line inside box: median (50th percentile)

  • "Whiskers" identify data within 1.5×IQR

  • Points beyond whiskers are outliers

    • common definition: Outlier>1.5×IQR

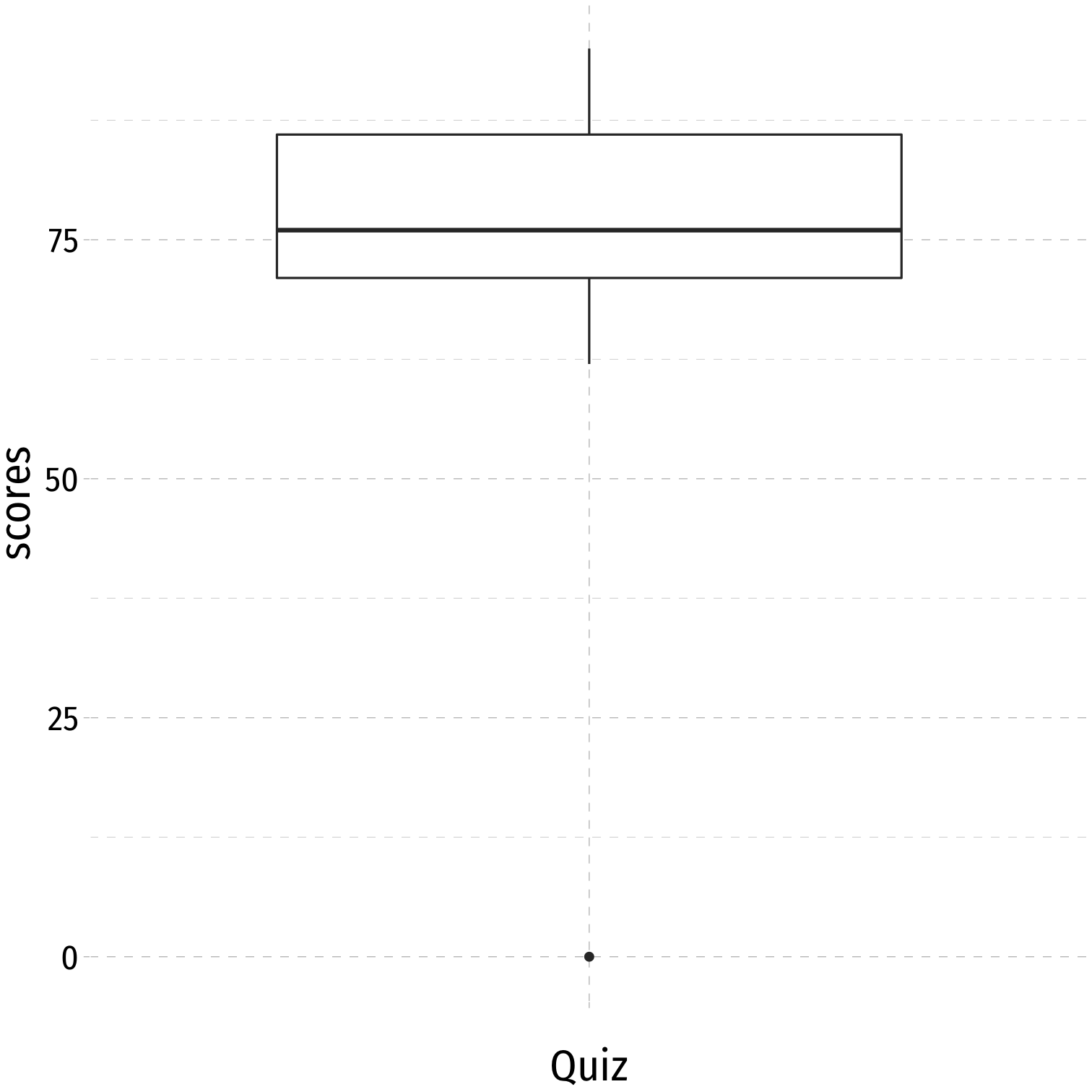
Comparisons I

  • Boxplots (and five number summaries) are great for comparing two distributions

Example:

Quiz 1:{0,62,66,71,71,74,76,79,83,86,88,93,95}Quiz 2:{50,62,72,73,79,81,82,82,86,90,94,98,99}

Comparisons II

quizzes_new %>% summary()
##     student       quiz_1          quiz_2     
##  Min.   : 1   Min.   : 0.00   Min.   :50.00  
##  1st Qu.: 4   1st Qu.:71.00   1st Qu.:73.00  
##  Median : 7   Median :76.00   Median :82.00  
##  Mean   : 7   Mean   :72.62   Mean   :80.62  
##  3rd Qu.:10   3rd Qu.:86.00   3rd Qu.:90.00  
##  Max.   :13   Max.   :95.00   Max.   :99.00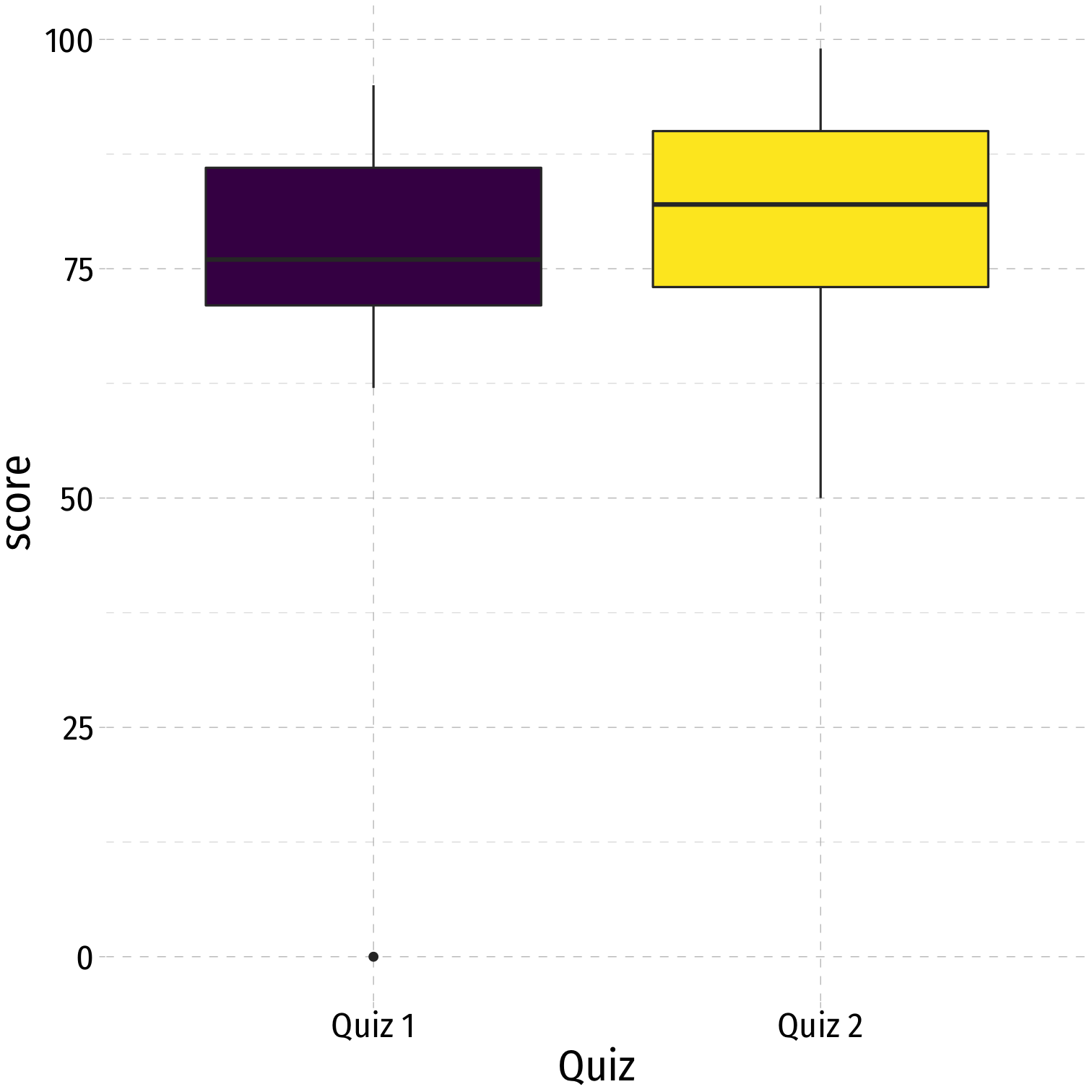

Aside: Making Nice Summary Tables I

  • I don't like the options available for printing out summary statistics

  • So I wrote my own R function called summary_table() that makes nice summary tables (it uses dplyr and tidyr!). To use:

  1. Download the summaries.R file from the website† and move it to your working directory/project folder

  2. Load the function with the source() command:‡

source("summaries.R")

† One day I'll make this part of a package I'll write.

‡ If it was a package, then you'd load with library(). But you can run a single .R script with source().

Aside: Making Nice Summary Tables II

3) The function has at least 2 arguments: the data.frame (automatically piped in if you use the pipe!) and then all variables you want to summarize, separated by commas†

mpg %>%
  summary_table(hwy, cty, cyl)
## # A tibble: 3 x 9
##   Variable   Obs   Min    Q1 Median    Q3   Max  Mean `Std. Dev.`
##   <chr>    <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl> <dbl>       <dbl>
## 1 cty        234     9    14     17    19    35 16.9         4.26
## 2 cyl        234     4     4      6     8     8  5.89        1.61
## 3 hwy        234    12    18     24    27    44 23.4         5.95

† There is one restriction: No variable name can have an underscore (_) in it. You will have to rename them or else you will break the function!

Aside: Making Nice Summary Tables II

4) When knitted in R markdown, it looks nicer:

mpg %>%
  summary_table(hwy, cty, cyl) %>%
  knitr::kable(., format="html")
Variable Obs Min Q1 Median Q3 Max Mean Std. Dev.
cty 234 9 14 17 19 35 16.86 4.26
cyl 234 4 4 6 8 8 5.89 1.61
hwy 234 12 18 24 27 44 23.44 5.95
  • We'll talk more about using markdown and making final products nicer when we discuss your paper project (have you forgotten?)

Measures of Dispersion: Deviations

  • Every observation i deviates from the mean of the data: deviationi=xi−μ

  • There are as many deviations as there are data points (n)

  • We can measure the average or standard deviation of a variable from its mean

  • Before we get there...

Variance (Population)

  • The population variance (σ2) of a population distribution measures the average of the squared deviations from the population mean (μ)

σ2=1NN∑i=1(xi−μ)2

  • Why do we square deviations?

  • What are these units?

Standard Deviation (Population)

  • Square root the variance to get the population standard deviation (σ), the average deviation from the population mean (in same units as x)

σ=√σ2=√1NN∑i=1(xi−μ)2

Variance (Sample)

  • The sample variance (s2) of a sample distribution measures the average of the squared deviations from the sample mean (ˉx)

σ2=1n−1n∑i=1(xi−ˉx)2

  • Why do we divide by n−1?

Standard Deviation (Sample)

  • Square root the sample variance to get the sample standard deviation (s), the average deviation from the sample mean (in same units as x)

s=√s2=√1n−1n∑i=1(xi−ˉx)2

Sample Standard Deviation: Example

Example: Calculate the sample standard deviation for the following series:

{2,4,6,8,10}

Sample Standard Deviation: Example

Example: Calculate the sample standard deviation for the following series:

{2,4,6,8,10}

sd(c(2,4,6,8,10))
## [1] 3.162278

The Steps to Calculate sd(), Coded I

#  first let's save our data in a tibble
sd_example<-tibble(x=c(2,4,6,8,10))
# first find the mean (just so we know)
sd_example %>%
  summarize(mean(x))
## # A tibble: 1 x 1
##   `mean(x)`
##       <dbl>
## 1         6
# now let's make some more columns:
sd_example <- sd_example %>%
  mutate(deviations = x-mean(x), # take deviations from mean
         deviations_sq = deviations^2) # square them

The Steps to Calculate sd(), Coded II

sd_example # see what we made
## # A tibble: 5 x 3
##       x deviations deviations_sq
##   <dbl>      <dbl>         <dbl>
## 1     2         -4            16
## 2     4         -2             4
## 3     6          0             0
## 4     8          2             4
## 5    10          4            16

The Steps to Calculate sd(), Coded III

sd_example %>%
  # sum the squared deviations
  summarize(sum_sq_devs = sum(deviations_sq), 
            # divide by n-1 to get variance
            variance = sum_sq_devs/(n()-1), 
            # square root to get sd
            std_dev = sqrt(variance))
## # A tibble: 1 x 3
##   sum_sq_devs variance std_dev
##         <dbl>    <dbl>   <dbl>
## 1          40       10    3.16

Sample Standard Deviation: You Try

You Try: Calculate the sample standard deviation for the following series:

{1,3,5,7}

Sample Standard Deviation: You Try

You Try: Calculate the sample standard deviation for the following series:

{1,3,5,7}

sd(c(1,3,5,7))
## [1] 2.581989

Descriptive Statistics: Populations vs. Samples

Population parameters

  • Population size: N

  • Mean: μ

  • Variance: σ2=1NN∑i=1(xi−μ)2

  • Standard deviation: σ=√σ2

Sample statistics

  • Population size: n

  • Mean: ˉx

  • Variance: s2=1n−1n∑i=1(xi−ˉx)2

  • Standard deviation: s=√s2

Outline

The Two Big Problems with Data

Data 101

Descriptive Statistics

Measures of Center

Measures of Dispersion

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow