2.3 — OLS Linear Regression
ECON 480 • Econometrics • Fall 2020
Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsF20
metricsF20.classes.ryansafner.com
Exploring Relationships
Bivariate Data and Relationships
- We looked at single variables for descriptive statistics
- Most uses of statistics in economics and business investigate relationships between variables
Examples
- # of police & crime rates
- healthcare spending & life expectancy
- government spending & GDP growth
- carbon dioxide emissions & temperatures

Bivariate Data and Relationships
We will begin with bivariate data for relationships between \(X\) and \(Y\)
Immediate aim is to explore associations between variables, quantified with correlation and linear regression
Later we want to develop more sophisticated tools to argue for causation

Bivariate Data: Spreadsheets I
econfreedom <- read_csv("econfreedom.csv")head(econfreedom)## # A tibble: 6 x 6## X1 Country ISO ef gdp continent## <dbl> <chr> <chr> <dbl> <dbl> <chr> ## 1 1 Albania ALB 7.4 4543. Europe ## 2 2 Algeria DZA 5.15 4784. Africa ## 3 3 Angola AGO 5.08 4153. Africa ## 4 4 Argentina ARG 4.81 10502. Americas ## 5 5 Australia AUS 7.93 54688. Oceania ## 6 6 Austria AUT 7.56 47604. Europe- Rows are individual observations (countries)
- Columns are variables on all individuals
Bivariate Data: Spreadsheets II
econfreedom %>% glimpse()## Rows: 112## Columns: 6## $ X1 <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, …## $ Country <chr> "Albania", "Algeria", "Angola", "Argentina", "Australia", "…## $ ISO <chr> "ALB", "DZA", "AGO", "ARG", "AUS", "AUT", "BHR", "BGD", "BE…## $ ef <dbl> 7.40, 5.15, 5.08, 4.81, 7.93, 7.56, 7.60, 6.35, 7.51, 6.22,…## $ gdp <dbl> 4543.0880, 4784.1943, 4153.1463, 10501.6603, 54688.4459, 47…## $ continent <chr> "Europe", "Africa", "Africa", "Americas", "Oceania", "Europ…Bivariate Data: Spreadsheets III
source("summaries.R") # use my summary_table functioneconfreedom %>% summary_table(ef, gdp)| Variable | Obs | Min | Q1 | Median | Q3 | Max | Mean | Std. Dev. |
|---|---|---|---|---|---|---|---|---|
| ef | 112 | 4.81 | 6.42 | 7.0 | 7.40 | 8.71 | 6.86 | 0.78 |
| gdp | 112 | 206.71 | 1307.46 | 5123.3 | 17302.66 | 89590.81 | 14488.49 | 19523.54 |
Bivariate Data: Scatterplots
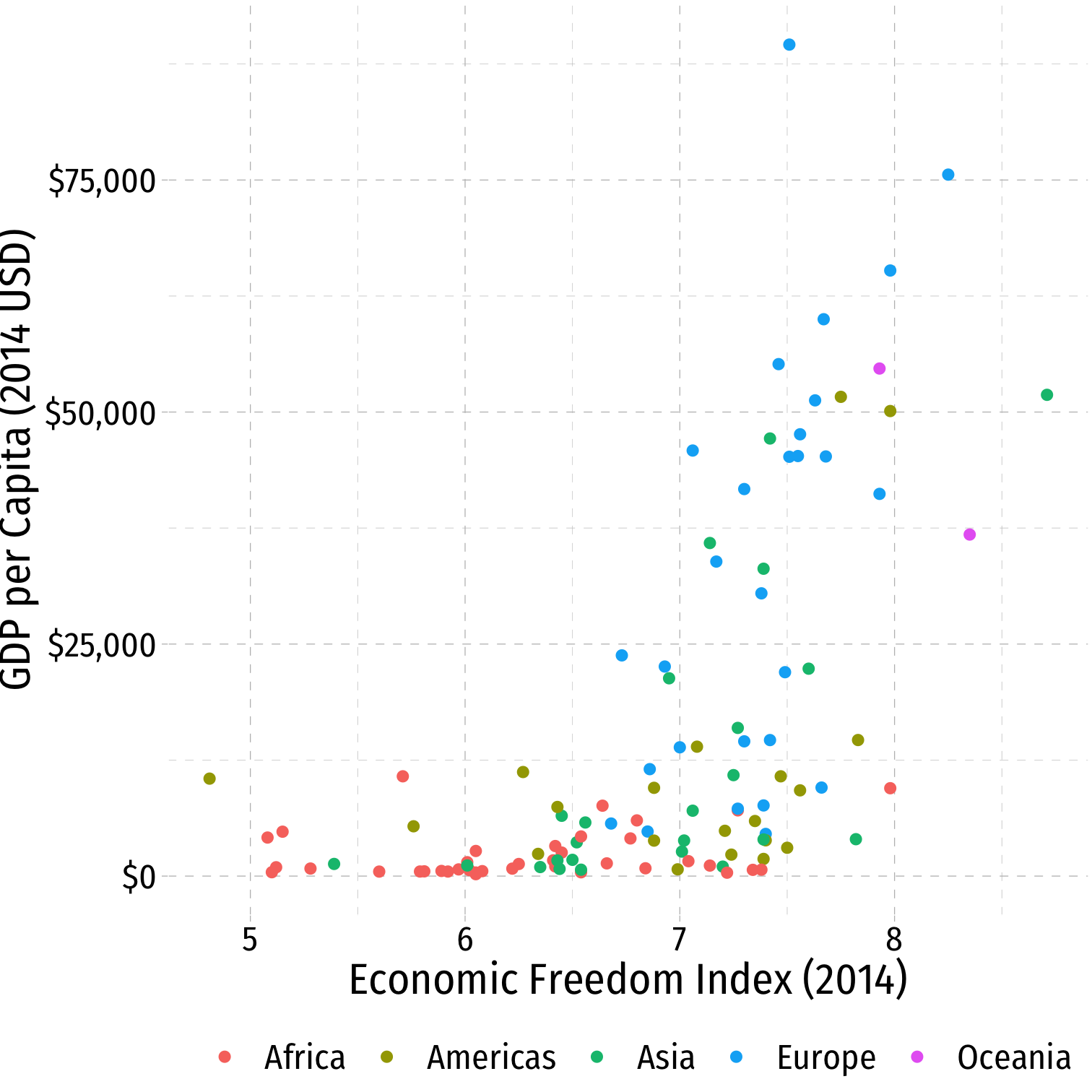
The best way to visualize an association between two variables is with a scatterplot
Each point: pair of variable values \((x_i,y_i) \in X, Y\) for observation \(i\)
library("ggplot2")ggplot(data = econfreedom)+ aes(x = ef, y = gdp)+ geom_point(aes(color = continent), size = 2)+ labs(x = "Economic Freedom Index (2014)", y = "GDP per Capita (2014 USD)", color = "")+ scale_y_continuous(labels = scales::dollar)+ theme_pander(base_family = "Fira Sans Condensed", base_size=20)+ theme(legend.position = "bottom")
Associations
- Look for association between independent and dependent variables
Direction: is the trend positive or negative?
Form: is the trend linear, quadratic, something else, or no pattern?
Strength: is the association strong or weak?
Outliers: do any observations break the trends above?
Quantifying Relationships
Covariance
- For any two variables, we can measure their sample covariance, \(cov(X,Y)\) or \(s_{X,Y}\) to quantify how they vary together†
Covariance
- For any two variables, we can measure their sample covariance, \(cov(X,Y)\) or \(s_{X,Y}\) to quantify how they vary together†
$$s_{X,Y}=E\big[(X-\bar{X})(Y-\bar{Y}) \big]$$
Covariance
- For any two variables, we can measure their sample covariance, \(cov(X,Y)\) or \(s_{X,Y}\) to quantify how they vary together†
$$s_{X,Y}=E\big[(X-\bar{X})(Y-\bar{Y}) \big]$$
- Intuition: if \(X\) is above its mean, would we expect \(Y\):
- to be above its mean also \((X\) and \(Y\) covary positively)
- to be below its mean \((X\) and \(Y\) covary negatively)
Covariance
- For any two variables, we can measure their sample covariance, \(cov(X,Y)\) or \(s_{X,Y}\) to quantify how they vary together†
$$s_{X,Y}=E\big[(X-\bar{X})(Y-\bar{Y}) \big]$$
- Intuition: if \(X\) is above its mean, would we expect \(Y\):
- to be above its mean also \((X\) and \(Y\) covary positively)
- to be below its mean \((X\) and \(Y\) covary negatively)
- Covariance is a common measure, but the units are meaningless, thus we rarely need to use it so don't worry about learning the formula
† Henceforth we limit all measures to samples, for convenience. Population covariance is denoted \(\sigma_{X,Y}\)
Covariance, in R
# base R cov(econfreedom$ef,econfreedom$gdp)## [1] 8922.933# dplyr econfreedom %>% summarize(cov = cov(ef,gdp))## # A tibble: 1 x 1## cov## <dbl>## 1 8923.Covariance, in R
# base R cov(econfreedom$ef,econfreedom$gdp)## [1] 8922.933# dplyr econfreedom %>% summarize(cov = cov(ef,gdp))## # A tibble: 1 x 1## cov## <dbl>## 1 8923.8923 what, exactly?
Correlation
- More convenient to standardize covariance into a more intuitive concept: correlation, \(\rho\) or \(r\) \(\in [-1, 1]\)
Correlation
- More convenient to standardize covariance into a more intuitive concept: correlation, \(\rho\) or \(r\) \(\in [-1, 1]\)
$$r_{X,Y}=\frac{s_{X,Y}}{s_X s_Y}=\frac{cov(X,Y)}{sd(X)sd(Y)}$$
Correlation
- More convenient to standardize covariance into a more intuitive concept: correlation, \(\rho\) or \(r\) \(\in [-1, 1]\)
$$r_{X,Y}=\frac{s_{X,Y}}{s_X s_Y}=\frac{cov(X,Y)}{sd(X)sd(Y)}$$
- Simply weight covariance by the product of the standard deviations of \(X\) and \(Y\)
Correlation
- More convenient to standardize covariance into a more intuitive concept: correlation, \(\rho\) or \(r\) \(\in [-1, 1]\)
$$r_{X,Y}=\frac{s_{X,Y}}{s_X s_Y}=\frac{cov(X,Y)}{sd(X)sd(Y)}$$
- Simply weight covariance by the product of the standard deviations of \(X\) and \(Y\)
- Alternatively, take the average† of the product of standardized \((Z\)-scores for) each \((x_i,y_i)\) pair:‡
Correlation
- More convenient to standardize covariance into a more intuitive concept: correlation, \(\rho\) or \(r\) \(\in [-1, 1]\)
$$r_{X,Y}=\frac{s_{X,Y}}{s_X s_Y}=\frac{cov(X,Y)}{sd(X)sd(Y)}$$
- Simply weight covariance by the product of the standard deviations of \(X\) and \(Y\)
- Alternatively, take the average† of the product of standardized \((Z\)-scores for) each \((x_i,y_i)\) pair:‡
$$\begin{align*} r&=\frac{1}{n-1}\sum^n_{i=1}\bigg(\frac{x_i-\bar{X}}{s_X}\bigg)\bigg(\frac{y_i-\bar{Y}}{s_Y}\bigg)\\ r&=\frac{1}{n-1}\sum^n_{i=1}Z_XZ_Y\\ \end{align*}$$
† Over n-1, a sample statistic!
‡ See today's class notes page for example code to calculate correlation "by hand" in R using the second method.
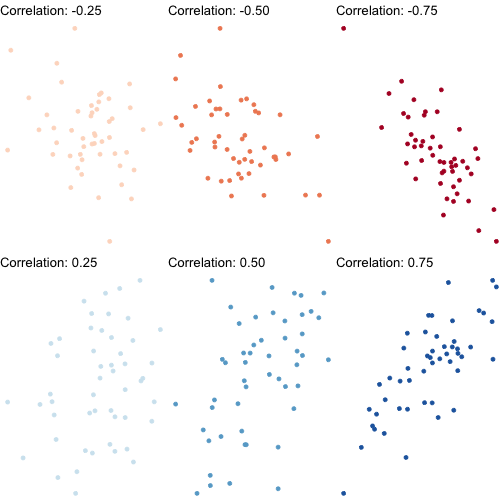
Correlation: Interpretation
- Correlation is standardized to
$$-1 \leq r \leq 1$$
Negative values \(\implies\) negative association
Positive values \(\implies\) positive association
Correlation of 0 \(\implies\) no association
As \(|r| \rightarrow 1 \implies\) the stronger the association
Correlation of \(|r|=1 \implies\) perfectly linear
Correlation and Covariance in R
# Base r: cov or cor(df$x, df$y)cov(econfreedom$ef, econfreedom$gdp)## [1] 8922.933cor(econfreedom$ef, econfreedom$gdp)## [1] 0.5867018Correlation and Covariance in R
# Base r: cov or cor(df$x, df$y)cov(econfreedom$ef, econfreedom$gdp)## [1] 8922.933cor(econfreedom$ef, econfreedom$gdp)## [1] 0.5867018# tidyverse method econfreedom %>% summarize(covariance = cov(ef, gdp), correlation = cor(ef, gdp))## # A tibble: 1 x 2## covariance correlation## <dbl> <dbl>## 1 8923. 0.587Correlation and Covariance in R I
corrplotis a great package (install and then load) to visualize correlations in data
library(corrplot) # see more at https://github.com/taiyun/corrplotlibrary(RColorBrewer) # for color scheme used herelibrary(gapminder) # for gapminder data# need to make a corelation matrix with cor(); can only include numeric variablesgapminder_cor<- gapminder %>% dplyr::select(gdpPercap, pop, lifeExp)# make a correlation table with cor (base R)gapminder_cor_table<-cor(gapminder_cor)# view itgapminder_cor_table## gdpPercap pop lifeExp## gdpPercap 1.00000000 -0.02559958 0.58370622## pop -0.02559958 1.00000000 0.06495537## lifeExp 0.58370622 0.06495537 1.00000000Correlation and Covariance in R II
corrplot(gapminder_cor_table, type="upper", method = "circle", order = "alphabet", col = viridis::viridis(100)) # custom colorCorrelation and Covariance in R II
corrplot(gapminder_cor_table, type="upper", method = "circle", order = "alphabet", col = viridis::viridis(100)) # custom color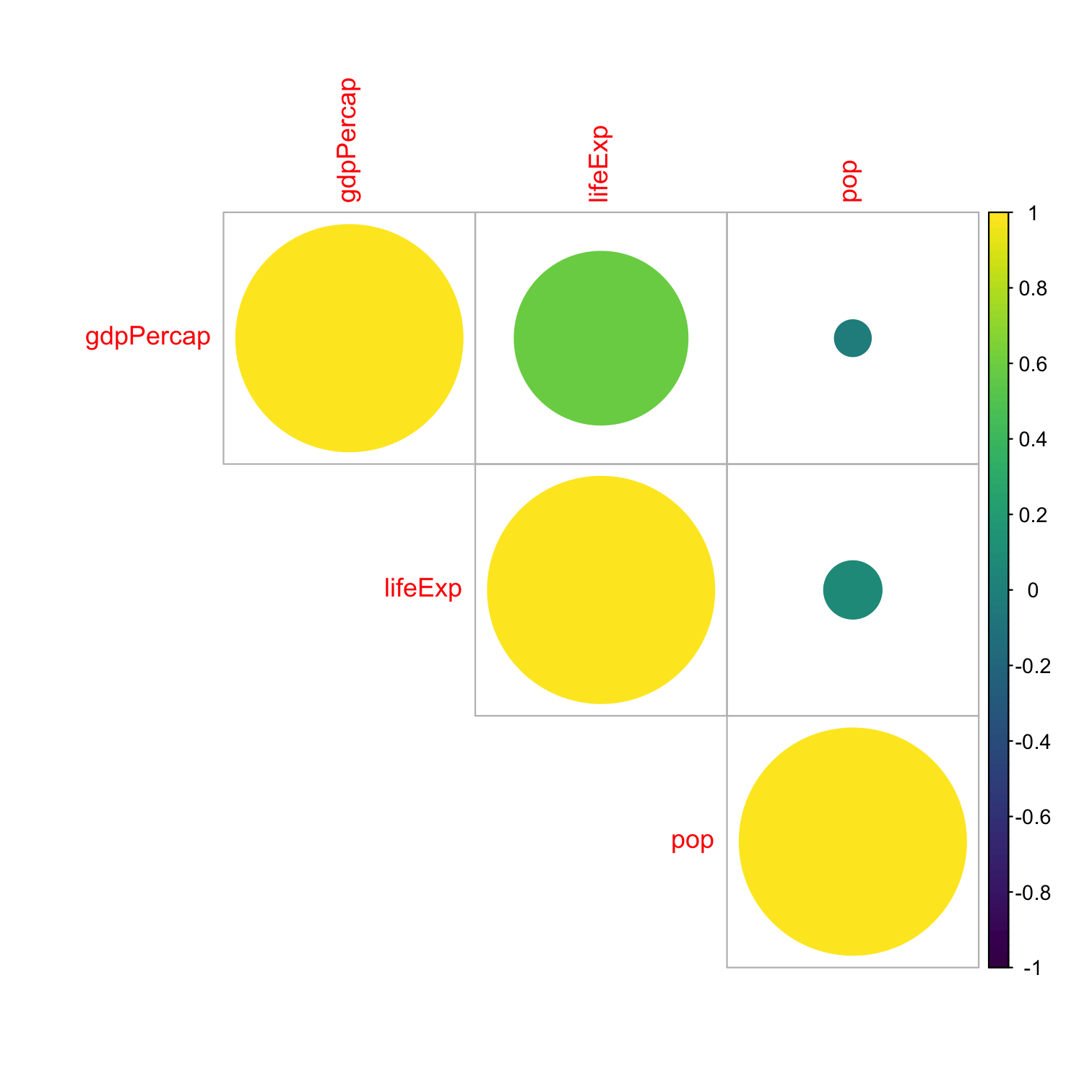
Correlation and Endogeneity
Your Occasional Reminder: Correlation does not imply causation!
- I'll show you the difference in a few weeks (when we can actually talk about causation)
If \(X\) and \(Y\) are strongly correlated, \(X\) can still be endogenous!
See today's class notes page for more on Covariance and Correlation

Always Plot Your Data!

Linear Regression
Fitting a Line to Data
- If an association appears linear, we can estimate the equation of a line that would "fit" the data
$$Y = a + bX$$
- Recall a linear equation describing a line contains:.magenta
- \(a\): vertical intercept
- \(b\): slope
Fitting a Line to Data
- If an association appears linear, we can estimate the equation of a line that would "fit" the data
$$Y = a + bX$$
Recall a linear equation describing a line contains:
- \(a\): vertical intercept
- \(b\): slope
How do we choose the equation that best fits the data?
Fitting a Line to Data
- If an association appears linear, we can estimate the equation of a line that would "fit" the data
$$Y = a + bX$$
Recall a linear equation describing a line contains:
- \(a\): vertical intercept
- \(b\): slope
How do we choose the equation that best fits the data?
This process is called linear regression
Population Linear Regression Model
Linear regression lets us estimate the slope of the population regression line between \(X\) and \(Y\) using sample data
We can make statistical inferences about the population slope coefficient
- eventually & hopefully: a causal inference
\(\text{slope}=\frac{\Delta Y}{\Delta X}\): for a 1-unit change in \(X\), how many units will this cause \(Y\) to change?
Class Size Example
Example: What is the relationship between class size and educational performance?

Class Size Example: Load the Data
# install.packages("haven") # install for first uselibrary("haven") # load for importing .dta filesCASchool<-read_dta("../data/caschool.dta")Class Size Example: Look at the Data I
glimpse(CASchool)## Rows: 420## Columns: 21## $ observat <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 1…## $ dist_cod <dbl> 75119, 61499, 61549, 61457, 61523, 62042, 68536, 63834, 6233…## $ county <chr> "Alameda", "Butte", "Butte", "Butte", "Butte", "Fresno", "Sa…## $ district <chr> "Sunol Glen Unified", "Manzanita Elementary", "Thermalito Un…## $ gr_span <chr> "KK-08", "KK-08", "KK-08", "KK-08", "KK-08", "KK-08", "KK-08…## $ enrl_tot <dbl> 195, 240, 1550, 243, 1335, 137, 195, 888, 379, 2247, 446, 98…## $ teachers <dbl> 10.90, 11.15, 82.90, 14.00, 71.50, 6.40, 10.00, 42.50, 19.00…## $ calw_pct <dbl> 0.5102, 15.4167, 55.0323, 36.4754, 33.1086, 12.3188, 12.9032…## $ meal_pct <dbl> 2.0408, 47.9167, 76.3226, 77.0492, 78.4270, 86.9565, 94.6237…## $ computer <dbl> 67, 101, 169, 85, 171, 25, 28, 66, 35, 0, 86, 56, 25, 0, 31,…## $ testscr <dbl> 690.80, 661.20, 643.60, 647.70, 640.85, 605.55, 606.75, 609.…## $ comp_stu <dbl> 0.34358975, 0.42083332, 0.10903226, 0.34979424, 0.12808989, …## $ expn_stu <dbl> 6384.911, 5099.381, 5501.955, 7101.831, 5235.988, 5580.147, …## $ str <dbl> 17.88991, 21.52466, 18.69723, 17.35714, 18.67133, 21.40625, …## $ avginc <dbl> 22.690001, 9.824000, 8.978000, 8.978000, 9.080333, 10.415000…## $ el_pct <dbl> 0.000000, 4.583333, 30.000002, 0.000000, 13.857677, 12.40875…## $ read_scr <dbl> 691.6, 660.5, 636.3, 651.9, 641.8, 605.7, 604.5, 605.5, 608.…## $ math_scr <dbl> 690.0, 661.9, 650.9, 643.5, 639.9, 605.4, 609.0, 612.5, 616.…## $ aowijef <dbl> 35.77982, 43.04933, 37.39445, 34.71429, 37.34266, 42.81250, …## $ es_pct <dbl> 1.000000, 3.583333, 29.000002, 1.000000, 12.857677, 11.40875…## $ es_frac <dbl> 0.01000000, 0.03583334, 0.29000002, 0.01000000, 0.12857677, …Class Size Example: Look at the Data II
| observat | dist_cod | county | district | gr_span | enrl_tot | teachers | calw_pct | meal_pct | computer | testscr | comp_stu | expn_stu | str | avginc | el_pct | read_scr | math_scr | aowijef | es_pct | es_frac |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 75119 | Alameda | Sunol Glen Unified | KK-08 | 195 | 10.90 | 0.5102 | 2.0408 | 67 | 690.80 | 0.3435898 | 6384.911 | 17.88991 | 22.690001 | 0.000000 | 691.6 | 690.0 | 35.77982 | 1.000000 | 0.0100000 |
| 2 | 61499 | Butte | Manzanita Elementary | KK-08 | 240 | 11.15 | 15.4167 | 47.9167 | 101 | 661.20 | 0.4208333 | 5099.381 | 21.52466 | 9.824000 | 4.583334 | 660.5 | 661.9 | 43.04933 | 3.583334 | 0.0358333 |
| 3 | 61549 | Butte | Thermalito Union Elementary | KK-08 | 1550 | 82.90 | 55.0323 | 76.3226 | 169 | 643.60 | 0.1090323 | 5501.955 | 18.69723 | 8.978000 | 30.000002 | 636.3 | 650.9 | 37.39445 | 29.000002 | 0.2900000 |
| 4 | 61457 | Butte | Golden Feather Union Elementary | KK-08 | 243 | 14.00 | 36.4754 | 77.0492 | 85 | 647.70 | 0.3497942 | 7101.831 | 17.35714 | 8.978000 | 0.000000 | 651.9 | 643.5 | 34.71429 | 1.000000 | 0.0100000 |
| 5 | 61523 | Butte | Palermo Union Elementary | KK-08 | 1335 | 71.50 | 33.1086 | 78.4270 | 171 | 640.85 | 0.1280899 | 5235.988 | 18.67133 | 9.080333 | 13.857677 | 641.8 | 639.9 | 37.34266 | 12.857677 | 0.1285768 |
| 6 | 62042 | Fresno | Burrel Union Elementary | KK-08 | 137 | 6.40 | 12.3188 | 86.9565 | 25 | 605.55 | 0.1824818 | 5580.147 | 21.40625 | 10.415000 | 12.408759 | 605.7 | 605.4 | 42.81250 | 11.408759 | 0.1140876 |
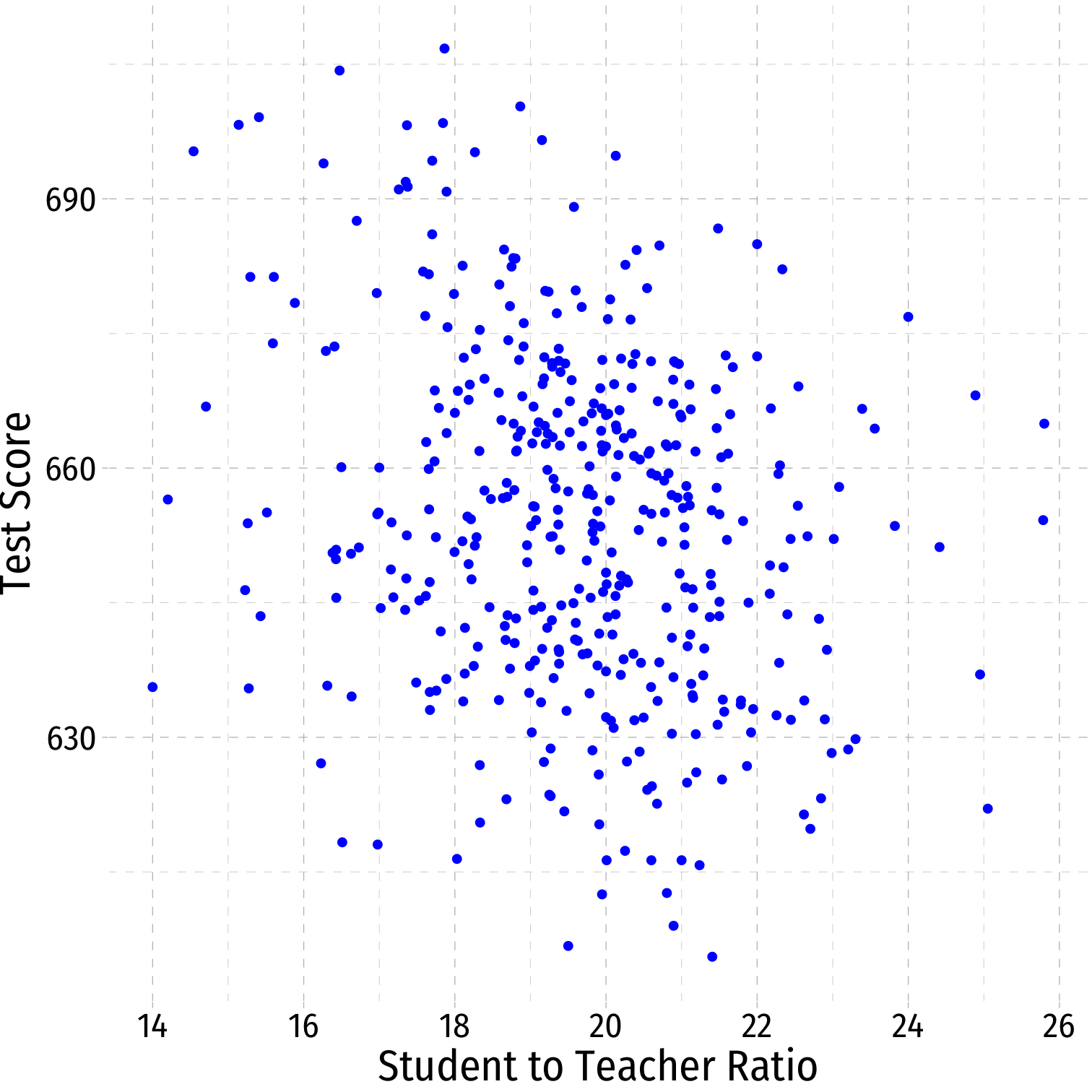
Class Size Example: Scatterplot
scatter <- ggplot(data = CASchool)+ aes(x = str, y = testscr)+ geom_point(color = "blue")+ labs(x = "Student to Teacher Ratio", y = "Test Score")+ theme_pander(base_family = "Fira Sans Condensed", base_size = 20)scatter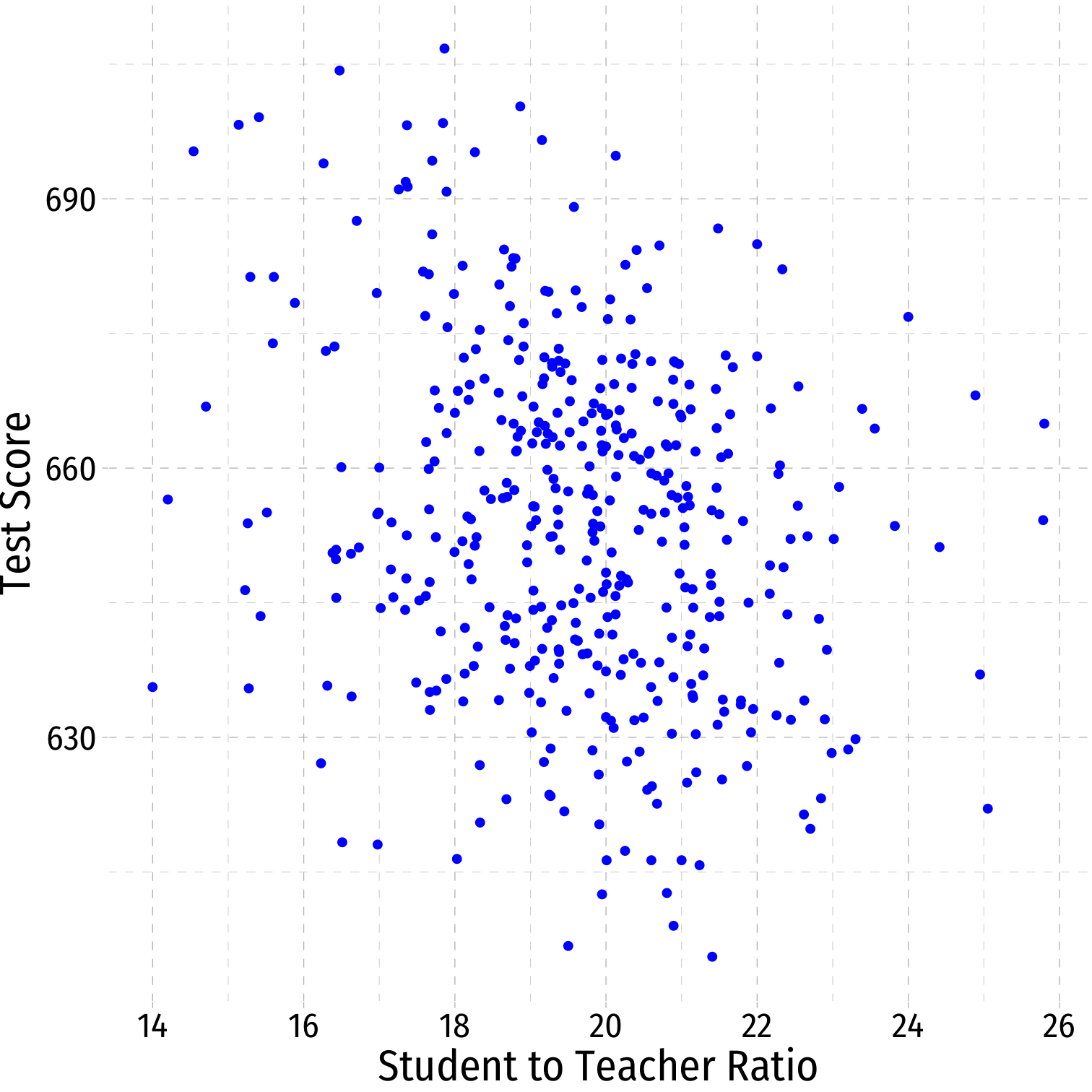
Class Size Example: Slope I
- If we change \((\Delta)\) the class size by an amount, what would we expect the change in test scores to be?
$$\beta = \frac{\text{change in test score}}{\text{change in class size}} = \frac{\Delta \text{test score}}{\Delta \text{class size}}$$
- If we knew \(\beta\), we could say that changing class size by 1 student will change test scores by \(\beta\)

Class Size Example: Slope II
- Rearranging:
$$\Delta \text{test score} = \beta \times \Delta \text{class size}$$

Class Size Example: Slope II
- Rearranging:
$$\Delta \text{test score} = \beta \times \Delta \text{class size}$$
- Suppose \(\beta=-0.6\). If we shrank class size by 2 students, our model predicts:
$$\begin{align*} \Delta \text{test score} &= -2 \times \beta\\ \Delta \text{test score} &= -2 \times -0.6\\ \Delta \text{test score}&= 1.2 \\ \end{align*}$$

Class Size Example: Slope and Average Effect
$$\text{test score} = \beta_0 + \beta_{1} \times \text{class size}$$
The line relating class size and test scores has the above equation
\(\beta_0\) is the vertical-intercept, test score where class size is 0
\(\beta_{1}\) is the slope of the regression line
This relationship only holds on average for all districts in the population, individual districts are also affected by other factors

Class Size Example: Marginal Effects
- To get an equation that holds for each district, we need to include other factors
$$\text{test score} = \beta_0 + \beta_1 \text{class size}+\text{other factors}$$
For now, we will ignore these until Unit III
Thus, \(\beta_0 + \beta_1 \text{class size}\) gives the average effect of class sizes on scores
Later, we will want to estimate the marginal effect (causal effect) of each factor on an individual district's test score, holding all other factors constant

Econometric Models Overview
$$Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + u$$
Econometric Models Overview
$$Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + u$$
- \(Y\) is the dependent variable of interest
- AKA "response variable," "regressand," "Left-hand side (LHS) variable"
Econometric Models Overview
$$Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + u$$
- \(Y\) is the dependent variable of interest
- AKA "response variable," "regressand," "Left-hand side (LHS) variable"
- \(X_1\) and \(X_2\) are independent variables
- AKA "explanatory variables", "regressors," "Right-hand side (RHS) variables", "covariates"
Econometric Models Overview
$$Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + u$$
- \(Y\) is the dependent variable of interest
- AKA "response variable," "regressand," "Left-hand side (LHS) variable"
- \(X_1\) and \(X_2\) are independent variables
- AKA "explanatory variables", "regressors," "Right-hand side (RHS) variables", "covariates"
- Our data consists of a spreadsheet of observed values of \((X_{1i}, X_{2i}, Y_i)\)
Econometric Models Overview
$$Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + u$$
- \(Y\) is the dependent variable of interest
- AKA "response variable," "regressand," "Left-hand side (LHS) variable"
- \(X_1\) and \(X_2\) are independent variables
- AKA "explanatory variables", "regressors," "Right-hand side (RHS) variables", "covariates"
- Our data consists of a spreadsheet of observed values of \((X_{1i}, X_{2i}, Y_i)\)
- To model, we "regress Y on \(X_1\) and \(X_2\)"
Econometric Models Overview
$$Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + u$$
- \(Y\) is the dependent variable of interest
- AKA "response variable," "regressand," "Left-hand side (LHS) variable"
- \(X_1\) and \(X_2\) are independent variables
- AKA "explanatory variables", "regressors," "Right-hand side (RHS) variables", "covariates"
- Our data consists of a spreadsheet of observed values of \((X_{1i}, X_{2i}, Y_i)\)
- To model, we "regress Y on \(X_1\) and \(X_2\)"
- \(\beta_0\) and \(\beta_1\) are parameters that describe the population relationships between the variables
- unknown! to be estimated!
Econometric Models Overview
$$Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + u$$
- \(Y\) is the dependent variable of interest
- AKA "response variable," "regressand," "Left-hand side (LHS) variable"
- \(X_1\) and \(X_2\) are independent variables
- AKA "explanatory variables", "regressors," "Right-hand side (RHS) variables", "covariates"
- Our data consists of a spreadsheet of observed values of \((X_{1i}, X_{2i}, Y_i)\)
- To model, we "regress Y on \(X_1\) and \(X_2\)"
- \(\beta_0\) and \(\beta_1\) are parameters that describe the population relationships between the variables
- unknown! to be estimated!
- \(u\) is the random error term
- 'U'nobservable, we can't measure it, and must model with assumptions about it
The Population Regression Model
How do we draw a line through the scatterplot? We do not know the "true" \(\beta_0\) or \(\beta_1\)
We do have data from a sample of class sizes and test scores†
So the real question is, how can we estimate \(\beta_0\) and \(\beta_1\)?
† Data are student-teacher-ratio and average test scores on Stanford 9 Achievement Test for 5th grade students for 420 K-6 and K-8 school districts in California in 1999, (Stock and Watson, 2015: p. 141)
Deriving OLS
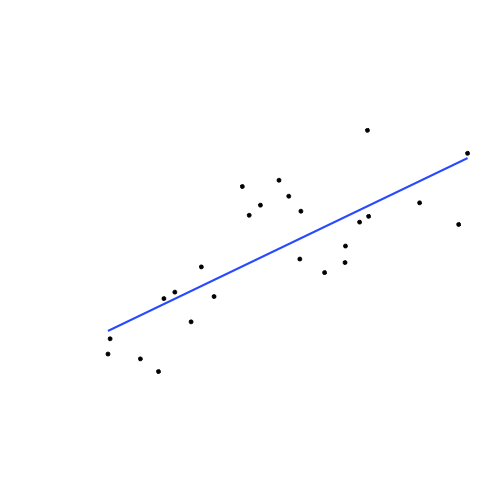
Deriving OLS
- Suppose we have some data points

Deriving OLS
- Suppose we have some data points
- We add a line
Deriving OLS
- Suppose we have some data points
- We add a line
- The residual, \(\hat{u}\) of each data point is the difference between the actual and the predicted value of \(Y\) given \(X\):
$$u_i = Y_i - \hat{Y_i}$$
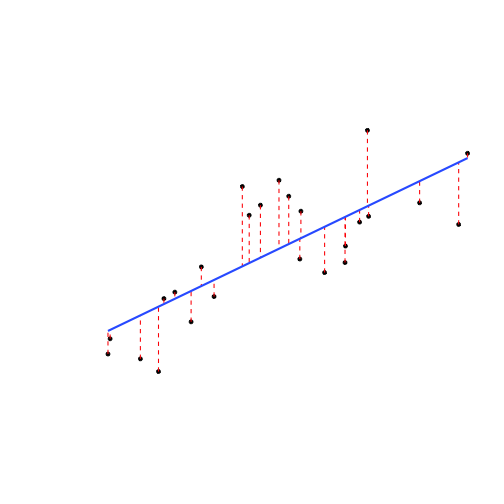
Deriving OLS
- Suppose we have some data points
- We add a line
- The residual, \(\hat{u}\) of each data point is the difference between the actual and the predicted value of \(Y\) given \(X\):
$$u_i = Y_i - \hat{Y_i}$$
- We square each residual
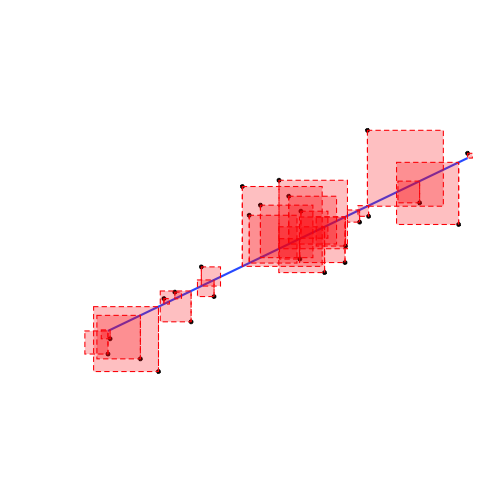
Deriving OLS
- Suppose we have some data points
- We add a line
- The residual, \(\hat{u}\) of each data point is the difference between the actual and the predicted value of \(Y\) given \(X\):
$$u_i = Y_i - \hat{Y_i}$$
- We square each residual
- Add all of these up: Sum of Squared Errors (SSE)
$$SSE = \sum^n_{i=1} u_i^2$$
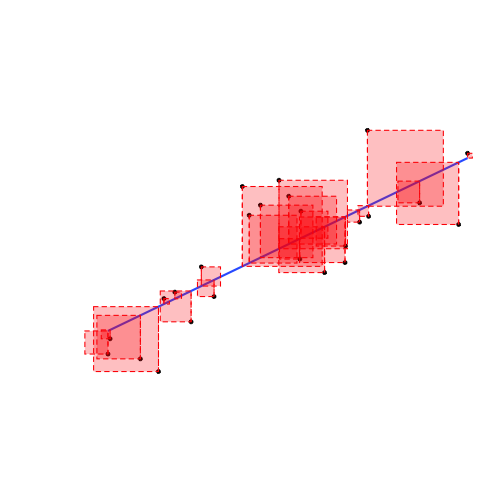
Deriving OLS
- Suppose we have some data points
- We add a line
- The residual, \(\hat{u}\) of each data point is the difference between the actual and the predicted value of \(Y\) given \(X\):
$$u_i = Y_i - \hat{Y_i}$$
- We square each residual
- Add all of these up: Sum of Squared Errors (SSE)
$$SSE = \sum^n_{i=1} u_i^2$$
- The line of best fit minimizes SSE
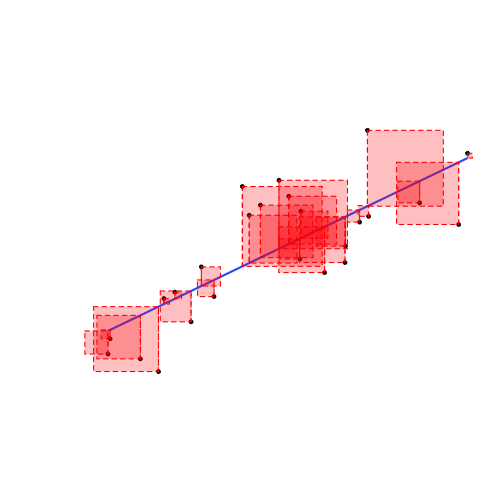
O rdinary L east S quares Estimators
- The Ordinary Least Squares (OLS) estimators of the unknown population parameters \(\beta_0\) and \(\beta_1\), solve the calculus problem:
$$\min_{\beta_0, \beta_1} \sum^n_{i=1}[\underbrace{Y_i-(\underbrace{\beta_0+\beta_1 X_i}_{\hat{Y_i}})}_{u}]^2$$
O rdinary L east S quares Estimators
- The Ordinary Least Squares (OLS) estimators of the unknown population parameters \(\beta_0\) and \(\beta_1\), solve the calculus problem:
$$\min_{\beta_0, \beta_1} \sum^n_{i=1}[\underbrace{Y_i-(\underbrace{\beta_0+\beta_1 X_i}_{\hat{Y_i}})}_{u}]^2$$
- Intuitively, OLS estimators minimize the average squared distance between the actual values \((Y_i)\) and the predicted values \((\hat{Y}_i)\) along the estimated regression line
The OLS Regression Line
- The OLS regression line or sample regression line is the linear function constructed using the OLS estimators:
$$\hat{Y_i}=\hat{\beta_0}+\hat{\beta_1}X_i$$
The OLS Regression Line
- The OLS regression line or sample regression line is the linear function constructed using the OLS estimators:
$$\hat{Y_i}=\hat{\beta_0}+\hat{\beta_1}X_i$$
- \(\hat{\beta_0}\) and \(\hat{\beta_1}\) ("beta 0 hat" & "beta 1 hat") are the OLS estimators of population parameters \(\beta_0\) and \(\beta_1\) using sample data
The OLS Regression Line
- The OLS regression line or sample regression line is the linear function constructed using the OLS estimators:
$$\hat{Y_i}=\hat{\beta_0}+\hat{\beta_1}X_i$$
\(\hat{\beta_0}\) and \(\hat{\beta_1}\) ("beta 0 hat" & "beta 1 hat") are the OLS estimators of population parameters \(\beta_0\) and \(\beta_1\) using sample data
The predicted value of Y given X, based on the regression, is \(E(Y_i|X_i)=\hat{Y_i}\)
The OLS Regression Line
- The OLS regression line or sample regression line is the linear function constructed using the OLS estimators:
$$\hat{Y_i}=\hat{\beta_0}+\hat{\beta_1}X_i$$
\(\hat{\beta_0}\) and \(\hat{\beta_1}\) ("beta 0 hat" & "beta 1 hat") are the OLS estimators of population parameters \(\beta_0\) and \(\beta_1\) using sample data
The predicted value of Y given X, based on the regression, is \(E(Y_i|X_i)=\hat{Y_i}\)
The residual or prediction error for the \(i^{th}\) observation is the difference between observed \(Y_i\) and its predicted value, \(\hat{u_i}=Y_i-\hat{Y_i}\)
The OLS Regression Estimators
- The solution to the SSE minimization problem yields:†
The OLS Regression Estimators
- The solution to the SSE minimization problem yields:†
$$\hat{\beta}_0=\bar{Y}-\hat{\beta_1}\bar{X}$$
The OLS Regression Estimators
- The solution to the SSE minimization problem yields:†
$$\hat{\beta}_0=\bar{Y}-\hat{\beta_1}\bar{X}$$
$$\hat{\beta}_1=\frac{\displaystyle\sum^n_{i=1}(X_i-\bar{X})(Y_i-\bar{Y})}{\displaystyle\sum^n_{i=1}(X_i-\bar{X})^2}=\frac{s_{XY}}{s^2_X}= \frac{cov(X,Y)}{var(X)}$$
† See next's class notes page for proofs.
Our Class Size Example in R
Class Size Scatterplot (Again)
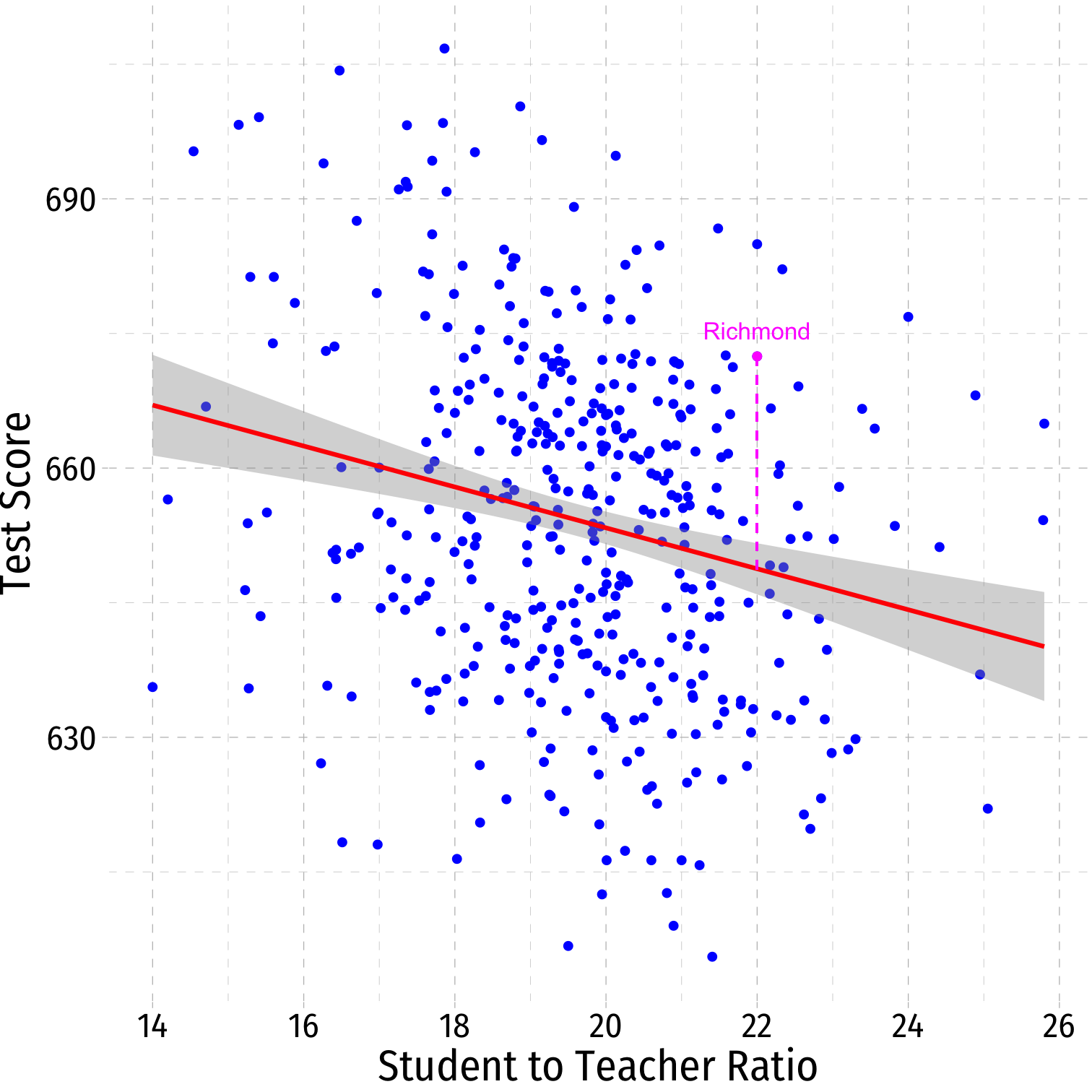
scatterThere is some true (unknown) population relationship: $$\text{test score}=\beta_0+\beta_1 \times str$$
\(\beta_1=\frac{\Delta \text{test score}}{\Delta \text{str}}= ??\)
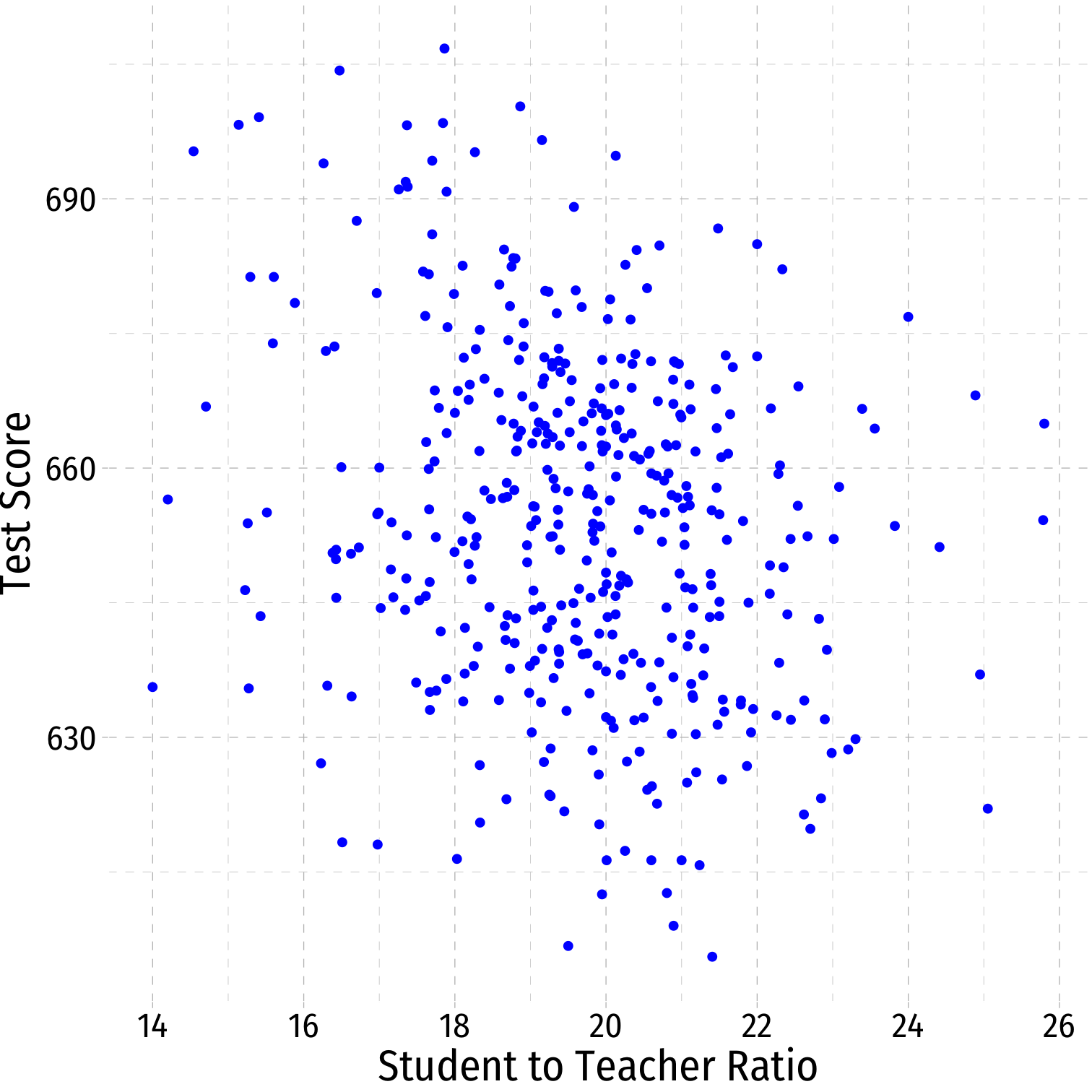
Class SIze Scatterplot with Regression Line
scatter+ geom_smooth(method = "lm", color = "red")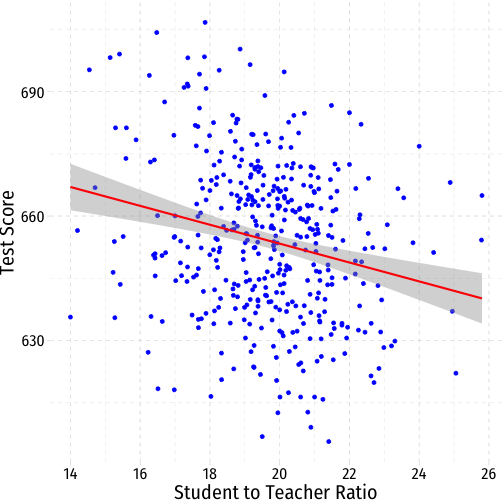
OLS in R
# run regression of testscr on strschool_reg <- lm(testscr ~ str, data = CASchool)Format for regression is lm(y ~ x, data = df)
yis dependent variable (listed first!)~means "modeled by" or "explained by"xis the independent variabledfis name of dataframe where data is stored
OLS in R II
# look at reg objectschool_reg## ## Call:## lm(formula = testscr ~ str, data = CASchool)## ## Coefficients:## (Intercept) str ## 698.93 -2.28- Stored as an
lmobject calledschool_reg, alistobject
OLS in R III
Looking at the
summary, there's a lot of information here!These objects are cumbersome, come from a much older, pre-
tidyverseepoch ofbase RLuckily, we now have
tidyways of working with regressions!
summary(school_reg) # get full summary## ## Call:## lm(formula = testscr ~ str, data = CASchool)## ## Residuals:## Min 1Q Median 3Q Max ## -47.727 -14.251 0.483 12.822 48.540 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 698.9330 9.4675 73.825 < 2e-16 ***## str -2.2798 0.4798 -4.751 2.78e-06 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 18.58 on 418 degrees of freedom## Multiple R-squared: 0.05124, Adjusted R-squared: 0.04897 ## F-statistic: 22.58 on 1 and 418 DF, p-value: 2.783e-06Tidy OLS in R: broom I

The
broompackage allows us to tidy up regression objects†The
tidy()function creates a tidytibbleof regression output
# load packageslibrary(broom)# tidy regression outputtidy(school_reg)## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 699. 9.47 73.8 6.57e-242## 2 str -2.28 0.480 -4.75 2.78e- 6Tidy OLS in R: broom II

The
broompackage allows us to tidy up regression objects†The
tidy()function creates a tidytibbleof regression output
# load packageslibrary(broom)# tidy regression output (with confidence intervals!)tidy(school_reg, conf.int = TRUE)## # A tibble: 2 x 7## term estimate std.error statistic p.value conf.low conf.high## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 699. 9.47 73.8 6.57e-242 680. 718. ## 2 str -2.28 0.480 -4.75 2.78e- 6 -3.22 -1.34More broom Tools: glance
glance()shows us a lot of overall regression statistics and diagnostics- We'll interpret these in the next lecture and beyond
# look at regression statistics and diagnosticsglance(school_reg)## # A tibble: 1 x 12## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 0.0512 0.0490 18.6 22.6 2.78e-6 1 -1822. 3650. 3663.## # … with 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>More broom Tools: augment
augment()creates useful new variables in the storedlmobject.fittedare fitted (predicted) values from model, i.e. \(\hat{Y}_i\).residare residuals (errors) from model, i.e. \(\hat{u}_i\)
# add regression-based values to dataaugment(school_reg)## # A tibble: 420 x 8## testscr str .fitted .resid .std.resid .hat .sigma .cooksd## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 691. 17.9 658. 32.7 1.76 0.00442 18.5 0.00689 ## 2 661. 21.5 650. 11.3 0.612 0.00475 18.6 0.000893## 3 644. 18.7 656. -12.7 -0.685 0.00297 18.6 0.000700## 4 648. 17.4 659. -11.7 -0.629 0.00586 18.6 0.00117 ## 5 641. 18.7 656. -15.5 -0.836 0.00301 18.6 0.00105 ## 6 606. 21.4 650. -44.6 -2.40 0.00446 18.5 0.0130 ## 7 607. 19.5 654. -47.7 -2.57 0.00239 18.5 0.00794 ## 8 609 20.9 651. -42.3 -2.28 0.00343 18.5 0.00895 ## 9 612. 19.9 653. -41.0 -2.21 0.00244 18.5 0.00597 ## 10 613. 20.8 652. -38.9 -2.09 0.00329 18.5 0.00723 ## # … with 410 more rowsClass Size Regression Result I
- Using OLS, we find: $$\widehat{\text{test score}}=689.9-2.28 \times str$$
Class Size Regression Result II
- There's a great package called
equatiomaticthat prints this equation inmarkdownor \(\LaTeX\).
$$ \operatorname{testscr} = 698.93 - 2.28(\operatorname{str}) + \epsilon $$
Class Size Regression Result II
- There's a great package called
equatiomaticthat prints this equation inmarkdownor \(\LaTeX\).
$$ \operatorname{testscr} = 698.93 - 2.28(\operatorname{str}) + \epsilon $$
Here was my code:
# install.packages("equatiomatic") # install for first uselibrary(equatiomatic) # load itextract_eq(school_reg, # regression lm object use_coefs = TRUE, # use names of variables coef_digits = 2, # round to 2 digits fix_signs = TRUE) # fix negatives (instead of + -)## $$## \operatorname{testscr} = 698.93 - 2.28(\operatorname{str}) + \epsilon## $$- In
Rchunk inR markdown, set{r, results="asis"}to print this raw output to be rendered
Class Size Regression: A Data Point
- One district in our sample is Richmond, CA:
CASchool %>% filter(district=="Richmond Elementary") %>% dplyr::select(district, testscr, str)## # A tibble: 1 x 3## district testscr str## <chr> <dbl> <dbl>## 1 Richmond Elementary 672. 22Predicted value: $$\widehat{\text{Test Score}}_{\text{Richmond}}=698-2.28(22) \approx 648$$
Residual $$\hat{u}_{Richmond}=672-648 \approx 24$$