+ - 0:00:00
Notes for current slide
Notes for next slide

2.5 — OLS: Precision and Diagnostics

ECON 480 • Econometrics • Fall 2020

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsF20
metricsF20.classes.ryansafner.com

Outline

Variation in ^β1

Presenting Regression Results

Diagnostics about Regression

Problem: Heteroskedasticity

Outliers

The Sampling Distribution of ^β1

^β1∼N(E[^β1],σ^β1)

  1. Center of the distribution (last class)
    • E[^β1]=β1†

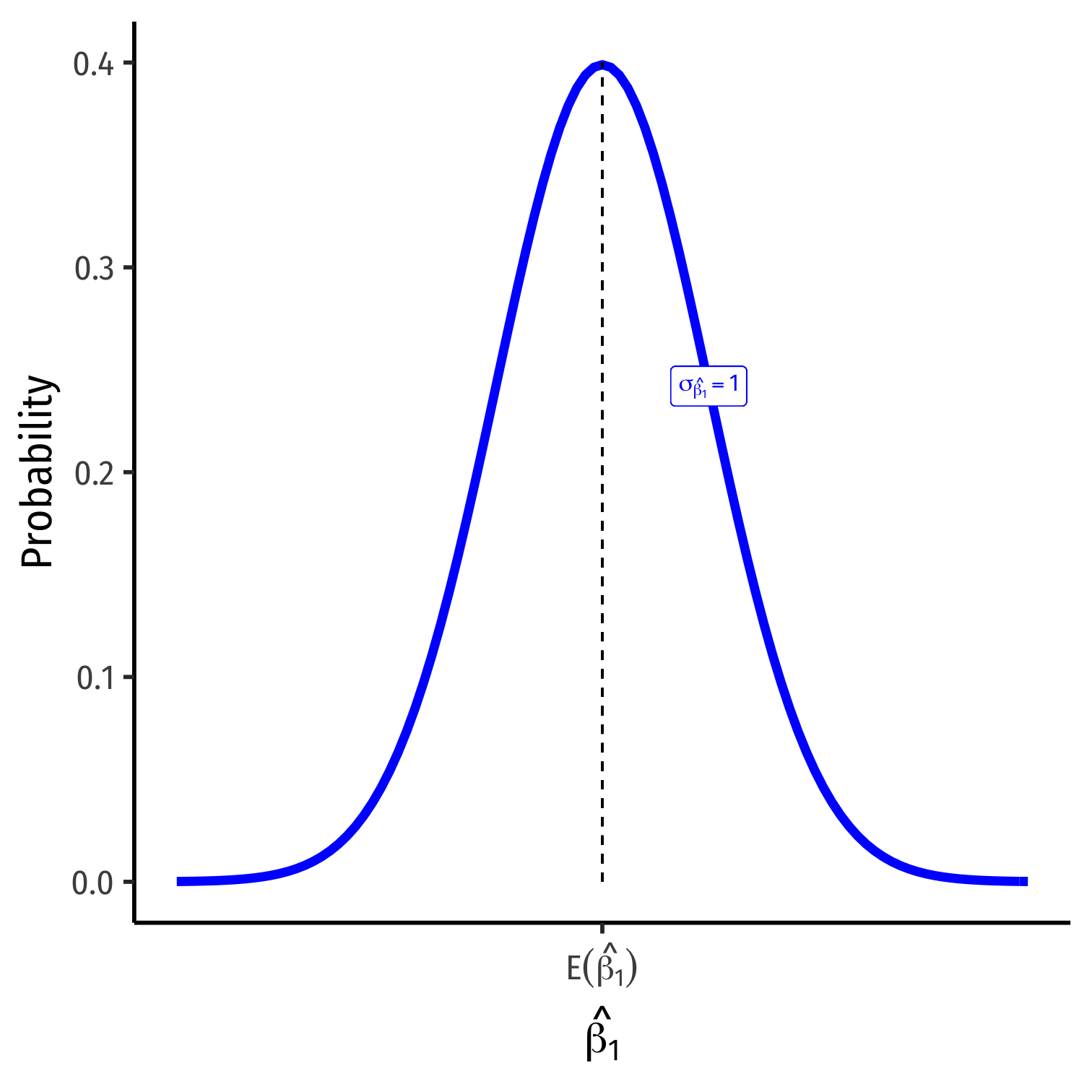
The Sampling Distribution of ^β1

^β1∼N(E[^β1],σ^β1)

  1. Center of the distribution (last class)

    • E[^β1]=β1†

  2. How precise is our estimate? (today)

    • Variance σ2^β1 or standard error‡ σ^β1

† Under the 4 assumptions about u (particularly, cor(X,u)=0).

‡ Standard “error” is the analog of standard deviation when talking about
the sampling distribution of a sample statistic (such as ˉX or ^β1).

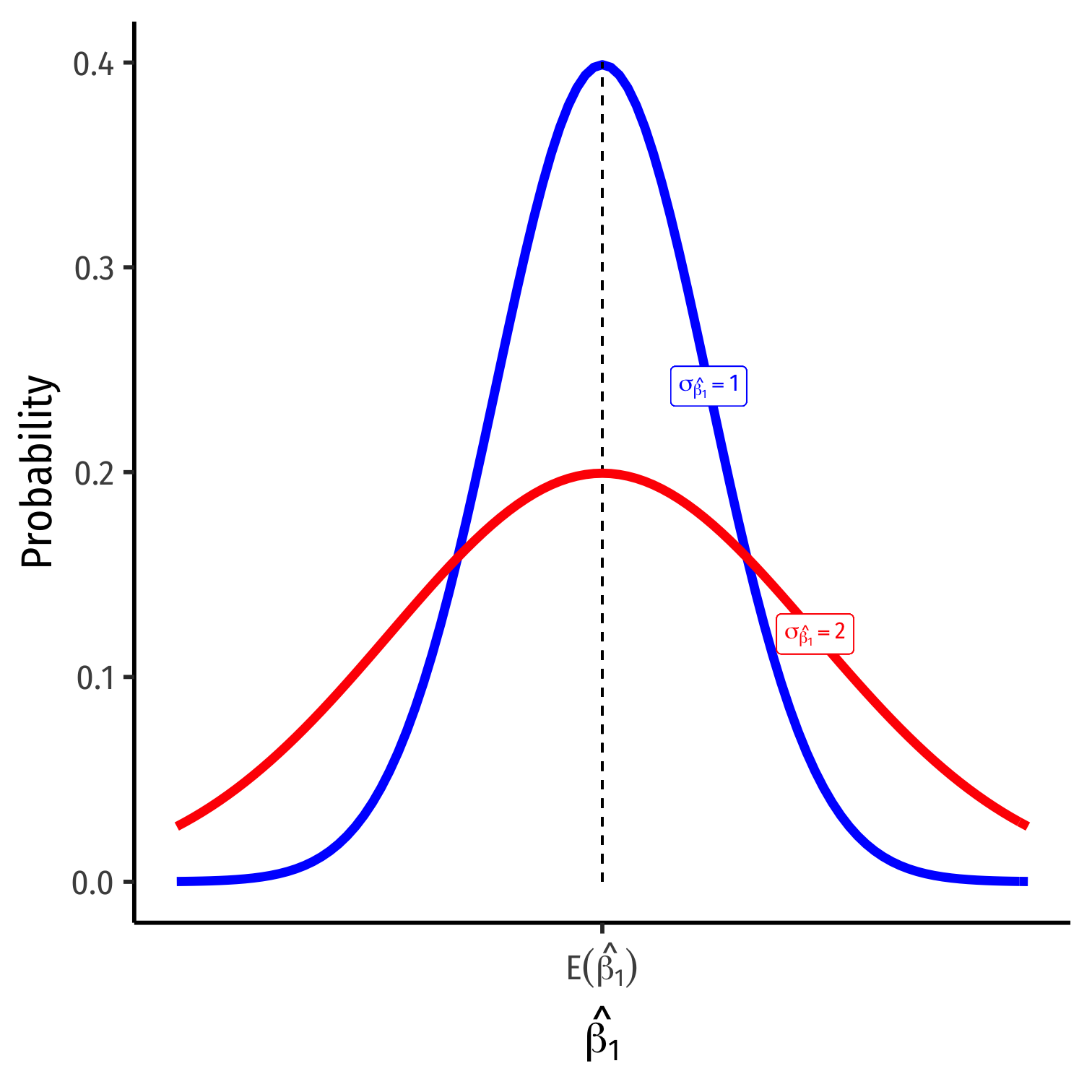
Variation in ^β1

What Affects Variation in ^β1

var(^β1)=(SER)2n×var(X)

se(^β1)=√var(^β1)=SER√n×sd(X)

  • Variation in ^β1 is affected by 3 things:
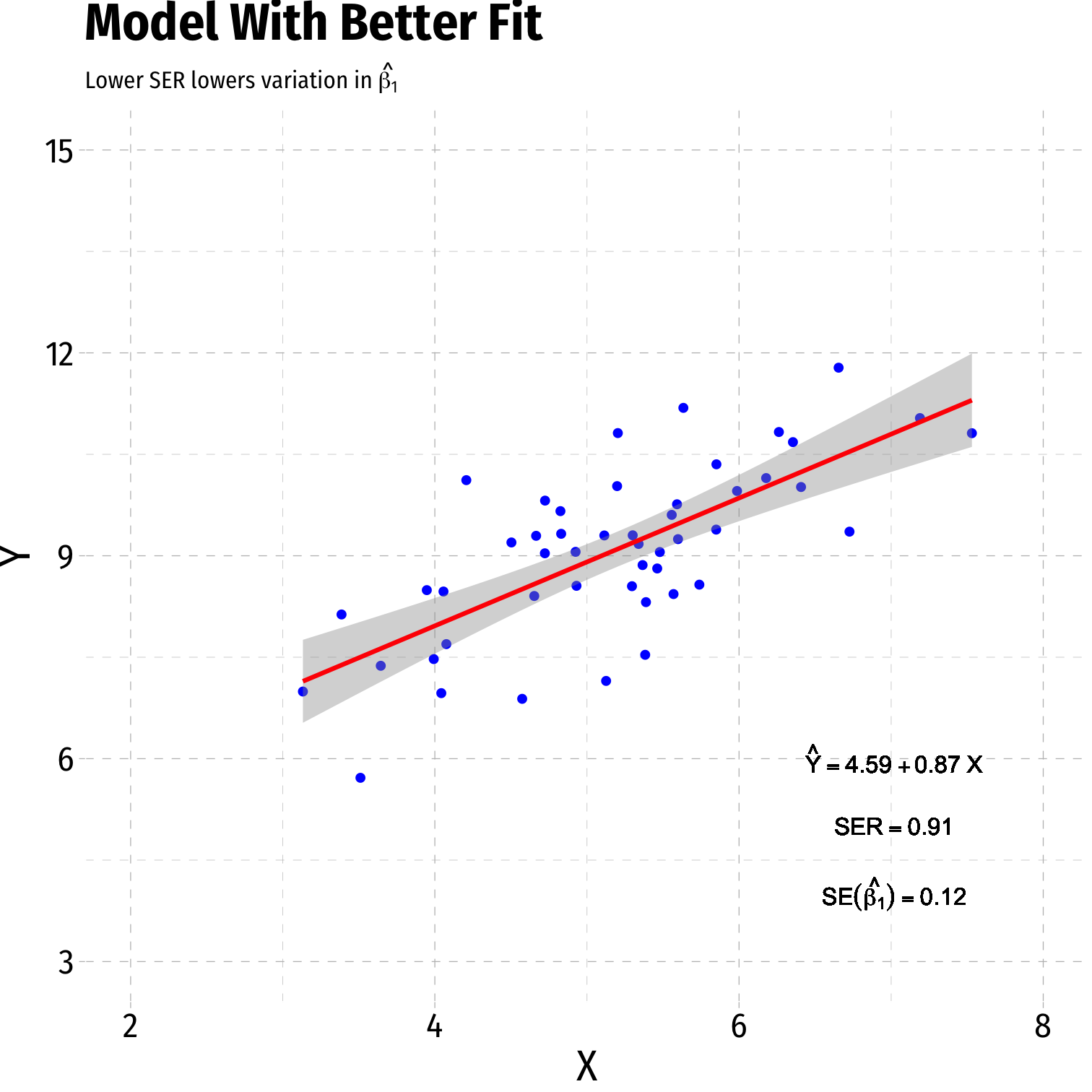
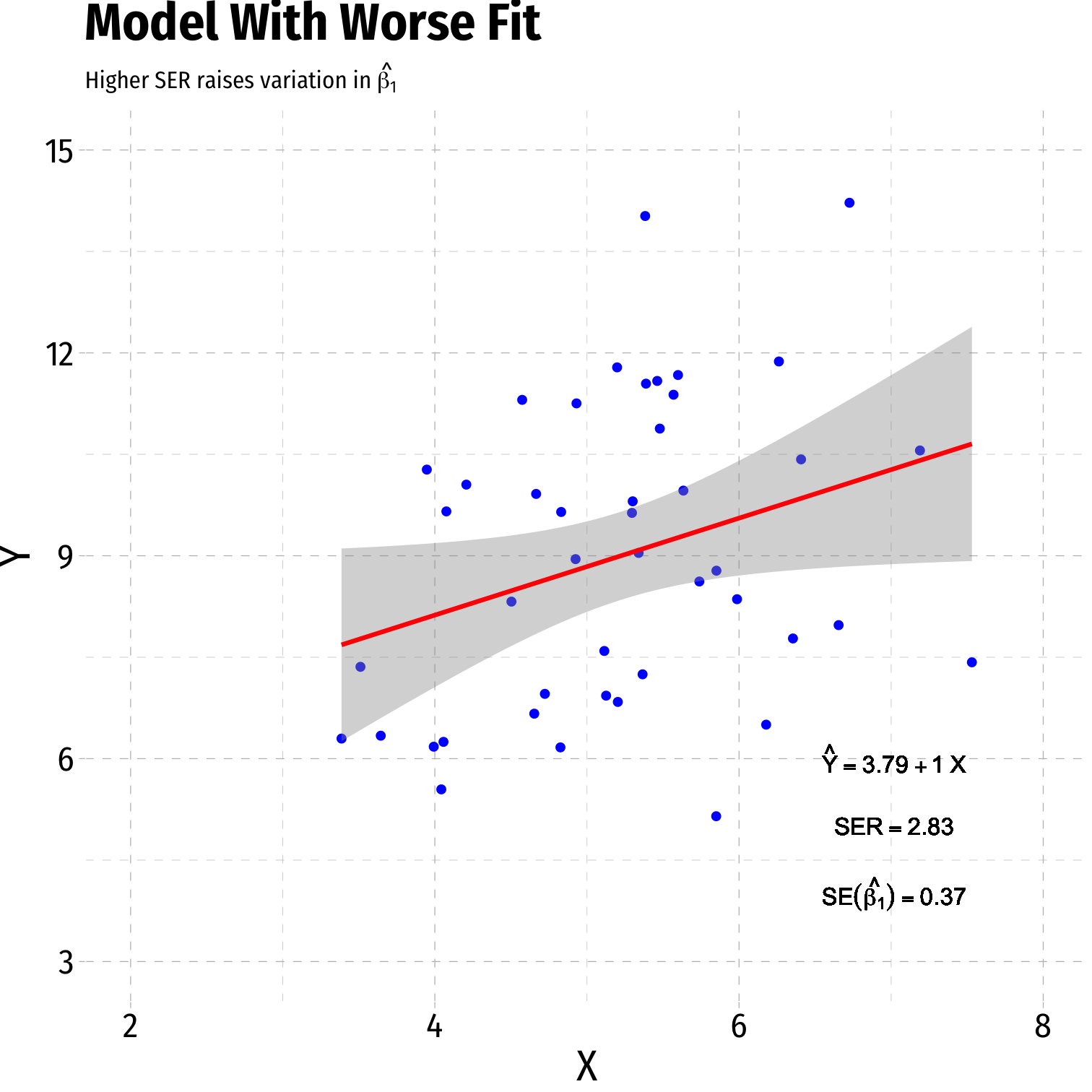
  1. Goodness of fit of the model (SER)†
    • Larger SER → larger var(^β1)
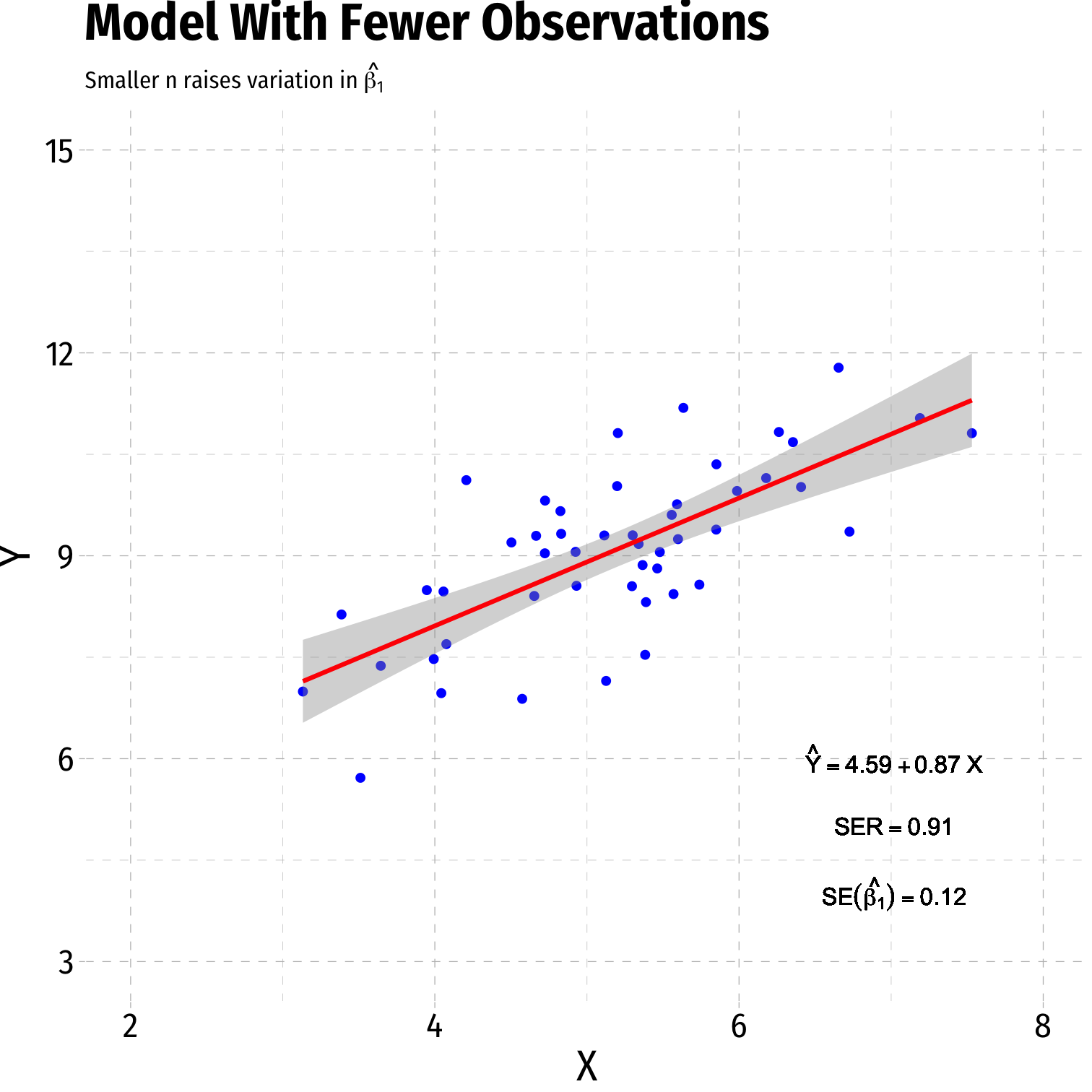
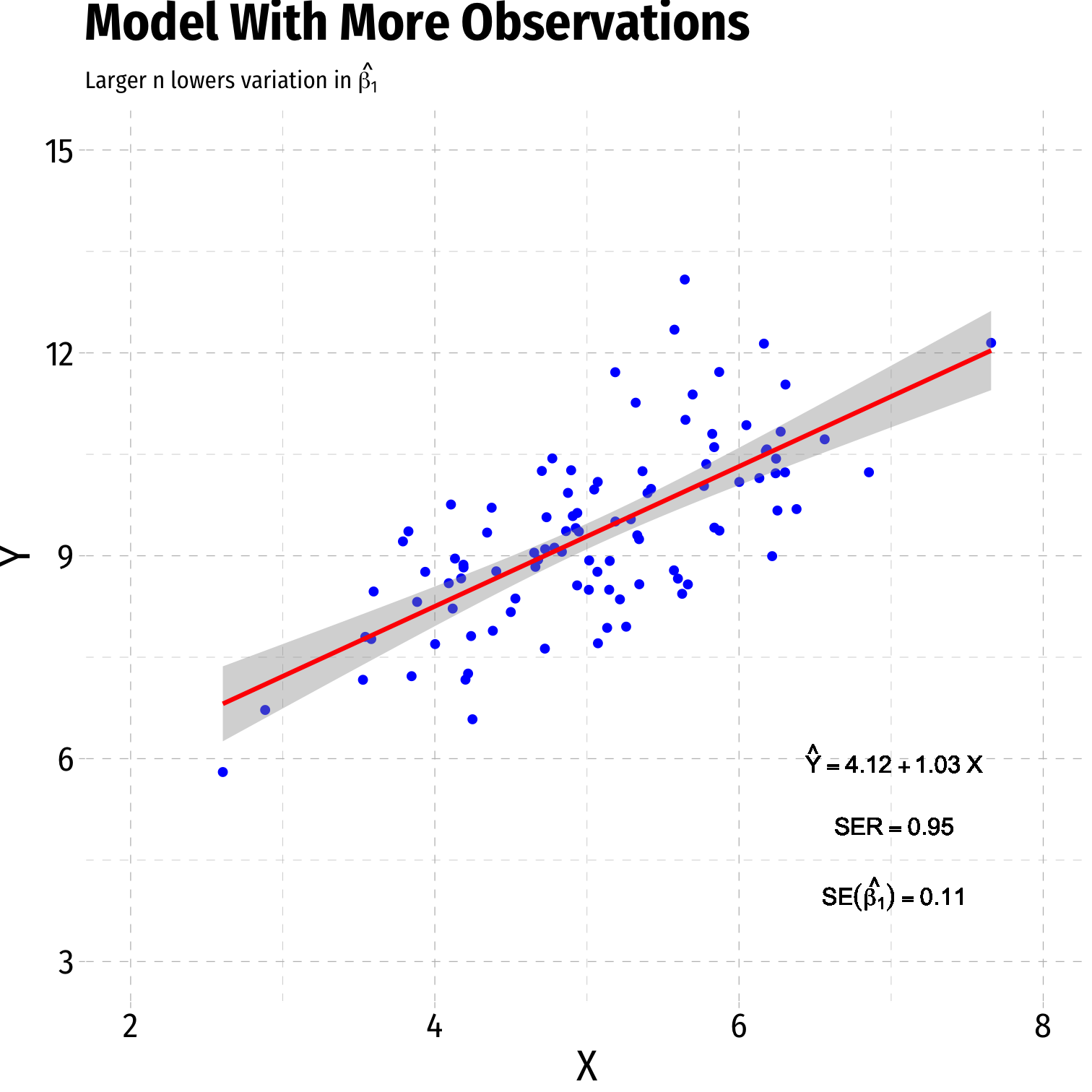
  2. Sample size, n
    • Larger n → smaller var(^β1)
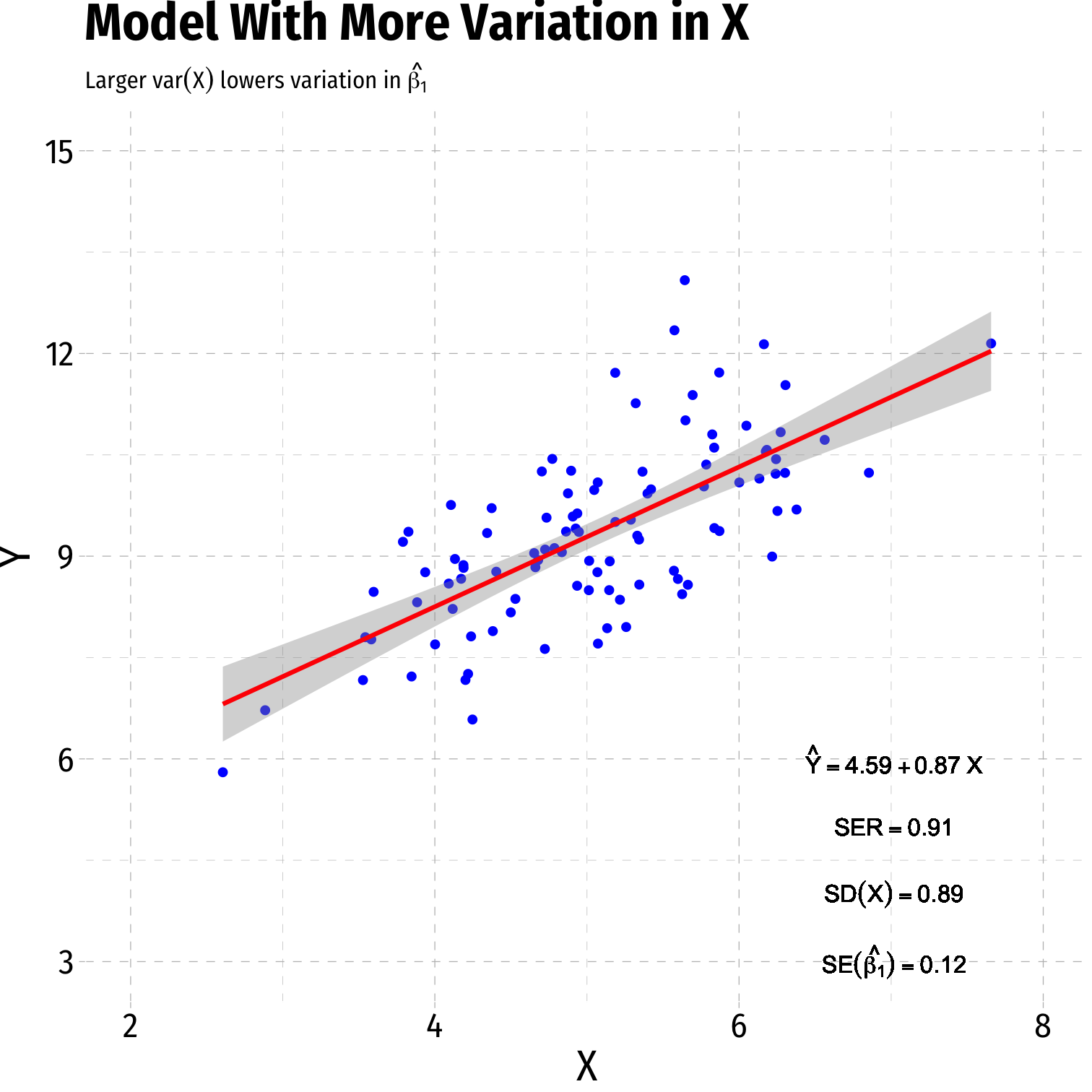
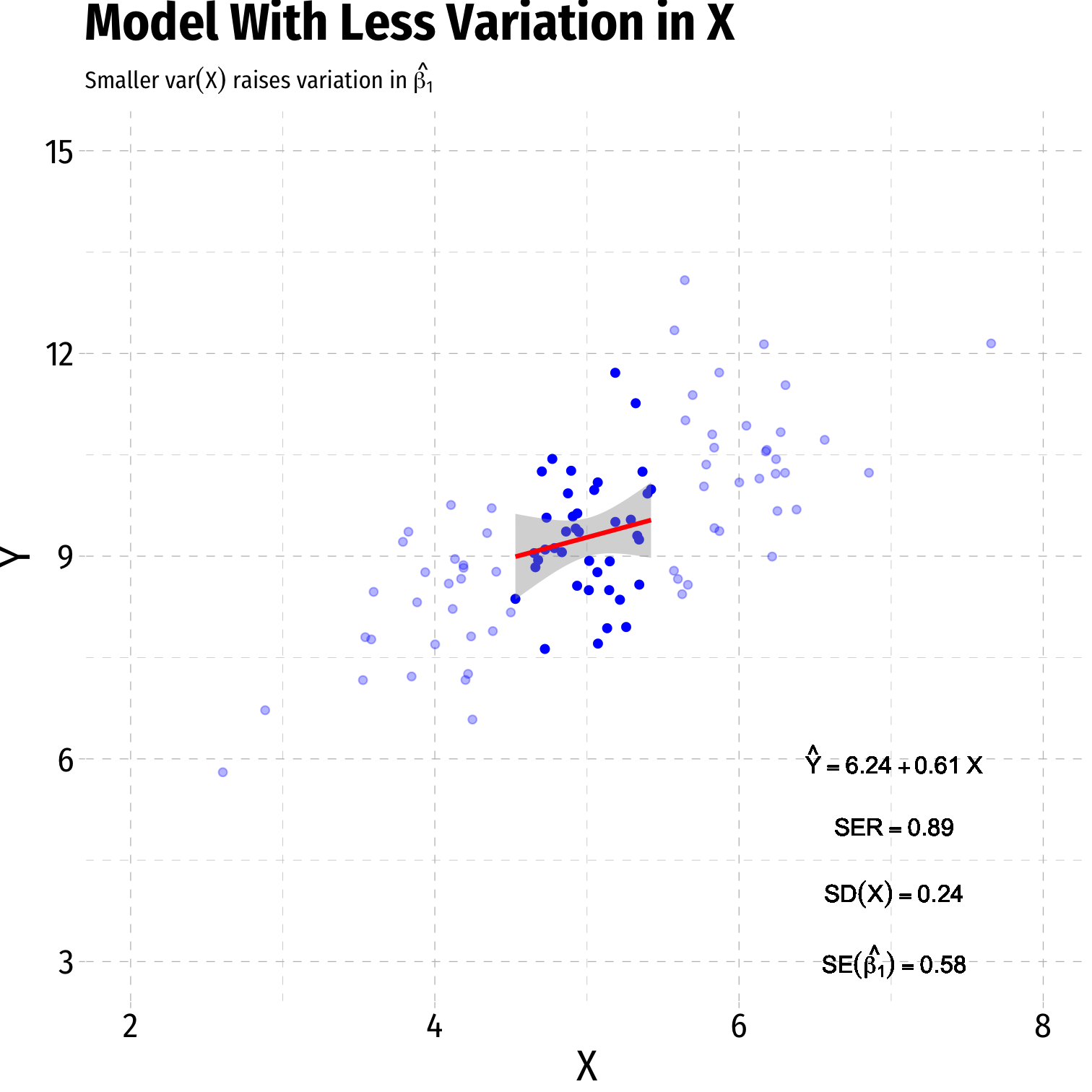
  3. Variance of X
    • Larger var(X) → smaller var(^β1)

† Recall from last class, the Standard Error of the Regression ^σu=√∑^ui2n−2

Variation in ^β1: Goodness of Fit

Variation in ^β1: Sample Size

Variation in ^β1: Variation in X

Presenting Regression Results

Our Class Size Regression: Base R

  • How can we present all of this information in a tidy way?
summary(school_reg) # get full summary
## 
## Call:
## lm(formula = testscr ~ str, data = CASchool)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -47.727 -14.251   0.483  12.822  48.540 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 698.9330     9.4675  73.825  < 2e-16 ***
## str          -2.2798     0.4798  -4.751 2.78e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 18.58 on 418 degrees of freedom
## Multiple R-squared:  0.05124,    Adjusted R-squared:  0.04897 
## F-statistic: 22.58 on 1 and 418 DF,  p-value: 2.783e-06

Our Class Size Regression: Broom I

  • broom's tidy() function creates a tidy tibble of regression output
# load broom
library(broom)
# tidy regression output
tidy(school_reg)
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
(Intercept)698.9329529.4674914
str-2.2798080.4798256
2 rows | 1-3 of 5 columns

Our Class Size Regression: Broom II

  • broom's glance() gives us summary statistics about the regression
glance(school_reg)
ABCDEFGHIJ0123456789
r.squared
<dbl>
adj.r.squared
<dbl>
sigma
<dbl>
statistic
<dbl>
p.value
<dbl>
df
<dbl>
0.05124010.0489703318.5809722.575112.783307e-061
1 row | 1-6 of 12 columns

Presenting Regressions in a Table

  • Professional journals and papers often have a regression table, including:

    • Estimates of ^β0 and ^β1
    • Standard errors of ^β0 and ^β1 (often below, in parentheses)
    • Indications of statistical significance (often with asterisks)
    • Measures of regression fit: R2, SER, etc

  • Later: multiple rows & columns for multiple variables & models

Test Score
Intercept698.93 ***
(9.47)   
STR-2.28 ***
(0.48)   
N420       
R-Squared0.05    
SER18.58    
*** p < 0.001; ** p < 0.01; * p < 0.05.

Regression Output with huxtable I

  • You will need to first install.packages("huxtable")

  • Load with library(huxtable)

  • Command: huxreg()

  • Main argument is the name of your lm object

  • Default output is fine, but often we want to customize a bit

# install.packages("huxtable")
library(huxtable)
huxreg(school_reg)
(1)
(Intercept)698.933 ***
(9.467)   
str-2.280 ***
(0.480)   
N420        
R20.051    
logLik-1822.250    
AIC3650.499    
*** p < 0.001; ** p < 0.01; * p < 0.05.

Regression Output with huxtable II

  • Can give title to each column
"Test Score" = school_reg

Regression Output with huxtable II

  • Can give title to each column
"Test Score" = school_reg
  • Can change name of coefficients from default
coefs = c("Intercept" = "(Intercept)",
          "STR" = "str")

Regression Output with huxtable II

  • Can give title to each column
"Test Score" = school_reg
  • Can change name of coefficients from default
coefs = c("Intercept" = "(Intercept)",
          "STR" = "str")
  • Decide what statistics to include, and rename them
statistics = c("N" = "nobs",
               "R-Squared" = "r.squared",
               "SER" = "sigma")

Regression Output with huxtable II

  • Can give title to each column
"Test Score" = school_reg
  • Can change name of coefficients from default
coefs = c("Intercept" = "(Intercept)",
          "STR" = "str")
  • Decide what statistics to include, and rename them
statistics = c("N" = "nobs",
               "R-Squared" = "r.squared",
               "SER" = "sigma")
  • Choose how many decimal places to round to
number_format = 2

Regression Output with huxtable III

huxreg("Test Score" = school_reg,
       coefs = c("Intercept" = "(Intercept)",
                 "STR" = "str"),
       statistics = c("N" = "nobs",
                      "R-Squared" = "r.squared",
                      "SER" = "sigma"),
       number_format = 2)

Regression Output with huxtable III

huxreg("Test Score" = school_reg,
       coefs = c("Intercept" = "(Intercept)",
                 "STR" = "str"),
       statistics = c("N" = "nobs",
                      "R-Squared" = "r.squared",
                      "SER" = "sigma"),
       number_format = 2)
Test Score
Intercept698.93 ***
(9.47)   
STR-2.28 ***
(0.48)   
N420       
R-Squared0.05    
SER18.58    
*** p < 0.001; ** p < 0.01; * p < 0.05.

Regression Outputs

  • huxtable is one package you can use

  • I used to only use stargazer, but as it was originally meant for STATA, it has limits and problems

Diagnostics about Regression

Diagnostics: Residuals I

  • We often look at the residuals of a regression to get more insight about its goodness of fit and its bias

  • Recall broom's augment creates some useful new variables

    • .fitted are fitted (predicted) values from model, i.e. ˆYi
    • .resid are residuals (errors) from model, i.e. ˆui

Diagnostics: Residuals II

  • Often a good idea to store in a new object (so we can make some plots)
aug_reg<-augment(school_reg)
aug_reg %>% head()
testscrstr.fitted.resid.std.resid.hat.sigma.cooksd
69117.965832.71.76 0.0044218.50.00689 
66121.565011.30.6120.0047518.60.000893
64418.7656-12.7-0.6850.0029718.60.0007  
64817.4659-11.7-0.6290.0058618.60.00117 
64118.7656-15.5-0.8360.0030118.60.00105 
60621.4650-44.6-2.4  0.0044618.50.013   

Recap: Assumptions about Errors

  • We make 4 critical assumptions about u:

  1. The expected value of the residuals is 0 E[u]=0

  2. The variance of the residuals over X is constant: var(u|X)=σ2u

  3. Errors are not correlated across observations: cor(ui,uj)=0∀i≠j

  4. There is no correlation between X and the error term: cor(X,u)=0 or E[u|X]=0

Assumptions 1 and 2: Errors are i.i.d.

  • Assumptions 1 and 2 assume that errors are coming from the same (normal) distribution u∼N(0,σu)

    • Assumption 1: E[u]=0
    • Assumption 2: sd(u|X)=σu
      • virtually always unknown...

  • We often can visually check by plotting a histogram of u

Plotting Residuals

ggplot(data = aug_reg)+
  aes(x = .resid)+
  geom_histogram(color="white", fill = "pink")+
  labs(x = expression(paste("Residual, ", hat(u))))+
  theme_pander(base_family = "Fira Sans Condensed",
           base_size=20)

Plotting Residuals

ggplot(data = aug_reg)+
  aes(x = .resid)+
  geom_histogram(color="white", fill = "pink")+
  labs(x = expression(paste("Residual, ", hat(u))))+
  theme_pander(base_family = "Fira Sans Condensed",
           base_size=20)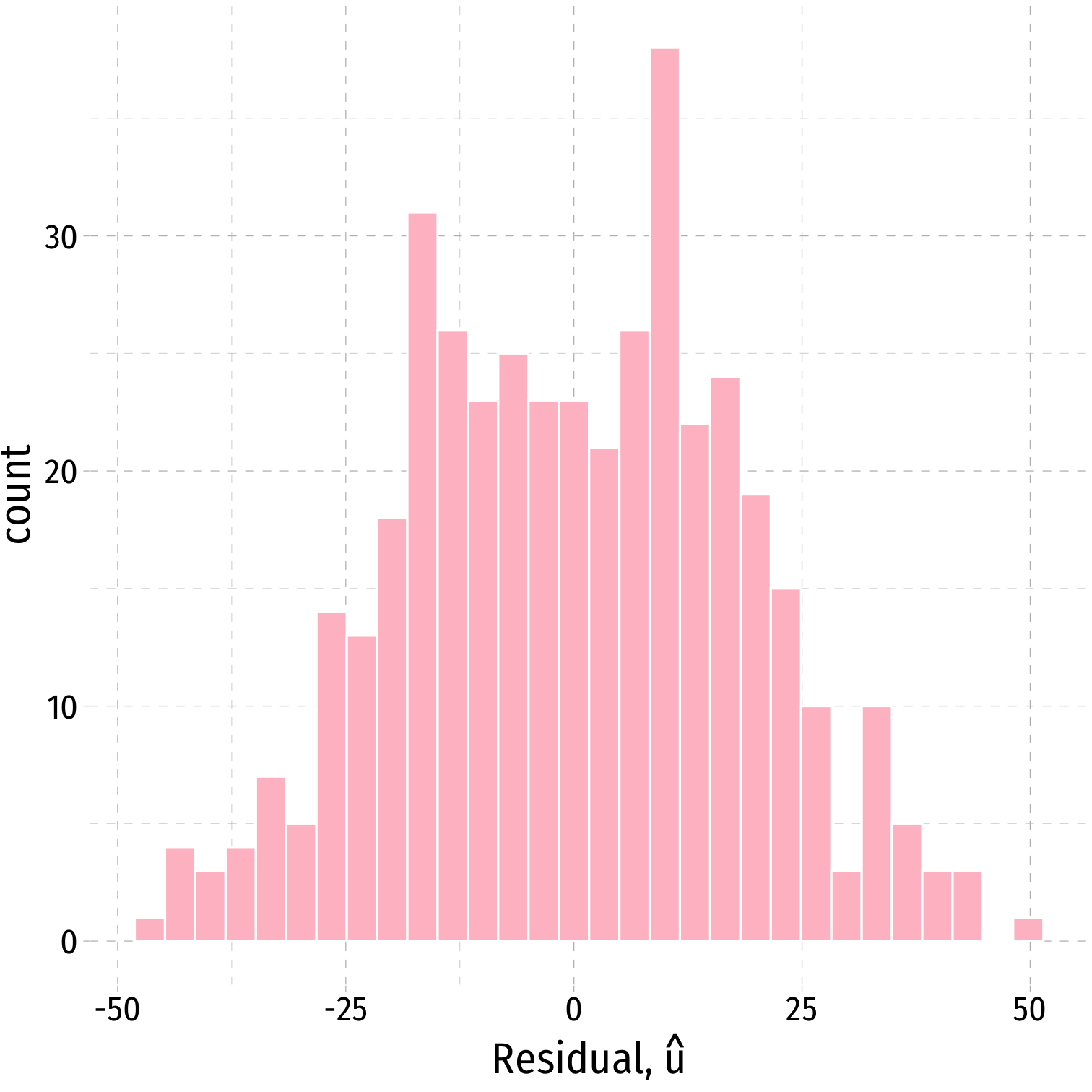

Plotting Residuals

ggplot(data = aug_reg)+
  aes(x = .resid)+
  geom_histogram(color="white", fill = "pink")+
  labs(x = expression(paste("Residual, ", hat(u))))+
  theme_pander(base_family = "Fira Sans Condensed",
           base_size=20)
  • Just to check:
aug_reg %>%
  summarize(E_u = mean(.resid),
            sd_u = sd(.resid))
E_usd_u
3.7e-1318.6

Residual Plot

  • We often plot a residual plot to see any odd patterns about residuals
    • x-axis are X values (str)
    • y-axis are u values (.resid)
ggplot(data = aug_reg)+
  aes(x = str,
      y = .resid)+
  geom_point(color="blue")+
  geom_hline(aes(yintercept = 0), color="red")+
  labs(x = "Student to Teacher Ratio",
       y = expression(paste("Residual, ", hat(u))))+
  theme_pander(base_family = "Fira Sans Condensed",
           base_size=20)

Residual Plot

  • We often plot a residual plot to see any odd patterns about residuals
    • x-axis are X values (str)
    • y-axis are u values (.resid)
ggplot(data = aug_reg)+
  aes(x = str,
      y = .resid)+
  geom_point(color="blue")+
  geom_hline(aes(yintercept = 0), color="red")+
  labs(x = "Student to Teacher Ratio",
       y = expression(paste("Residual, ", hat(u))))+
  theme_pander(base_family = "Fira Sans Condensed",
           base_size=20)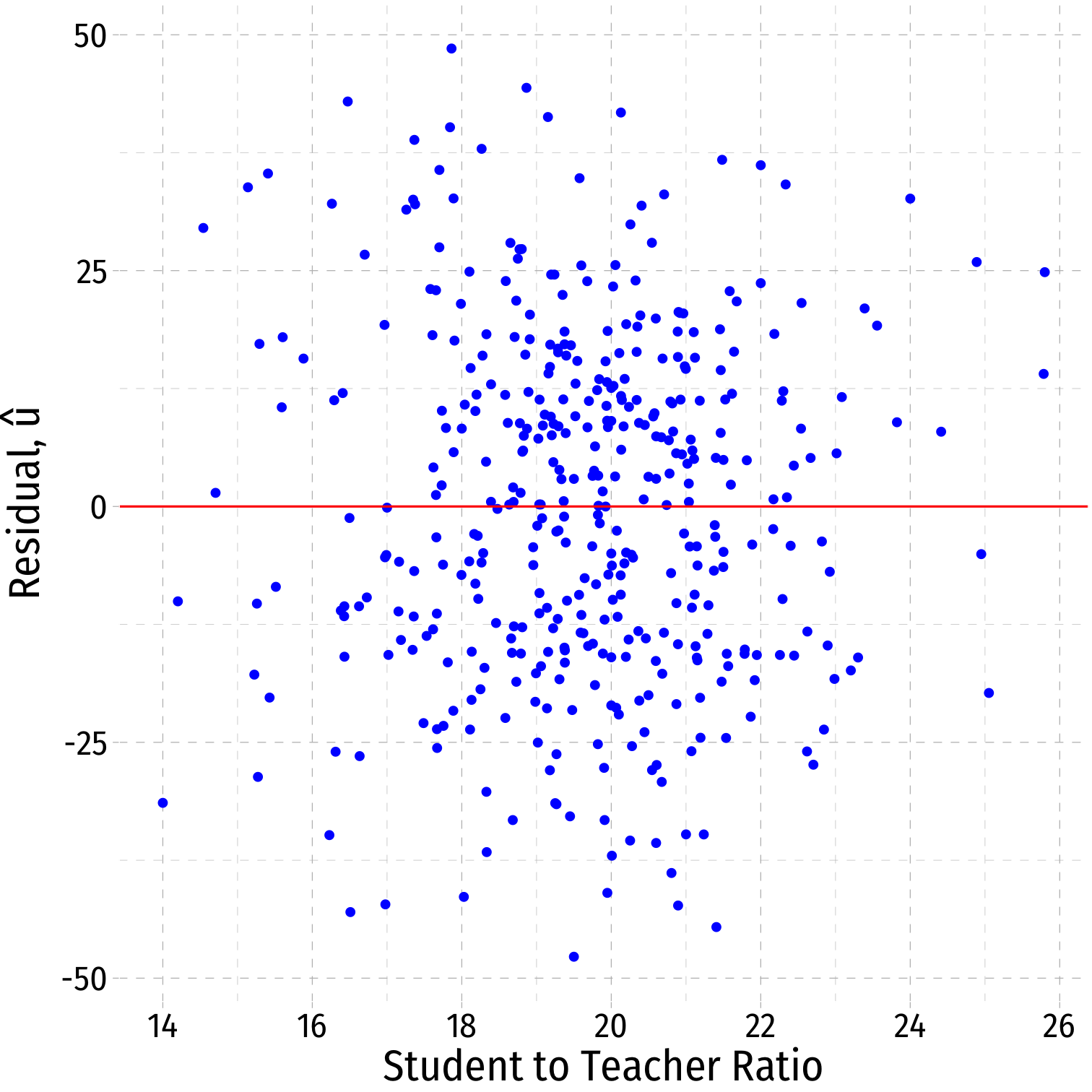

Problem: Heteroskedasticity

Homoskedasticity

  • "Homoskedasticity:" variance of the residuals over X is constant, written: var(u|X)=σ2u

  • Knowing the value of X does not affect the variance (spread) of the errors

Heteroskedasticity I

  • "Heteroskedasticity:" variance of the residuals over X is NOT constant: var(u|X)≠σ2u

  • This does not cause ^β1 to be biased, but it does cause the standard error of ^β1 to be incorrect

  • This does cause a problem for inference!

Heteroskedasticity II

  • Recall the formula for the standard error of ^β1:

se(^β1)=√var(^β1)=SER√n×sd(X)

  • This actually assumes homoskedasticity

Heteroskedasticity III

  • Under heteroskedasticity, the standard error of ^β1 mutates to:

se(^β1)=√n∑i=1(Xi−ˉX)2ˆu2[n∑i=1(Xi−ˉX)2]2

  • This is a heteroskedasticity-robust (or just "robust") method of calculating se(^β1)

  • Don't learn formula, do learn what heteroskedasticity is and how it affects our model!

Visualizing Heteroskedasticity I

  • Our original scatterplot with regression line

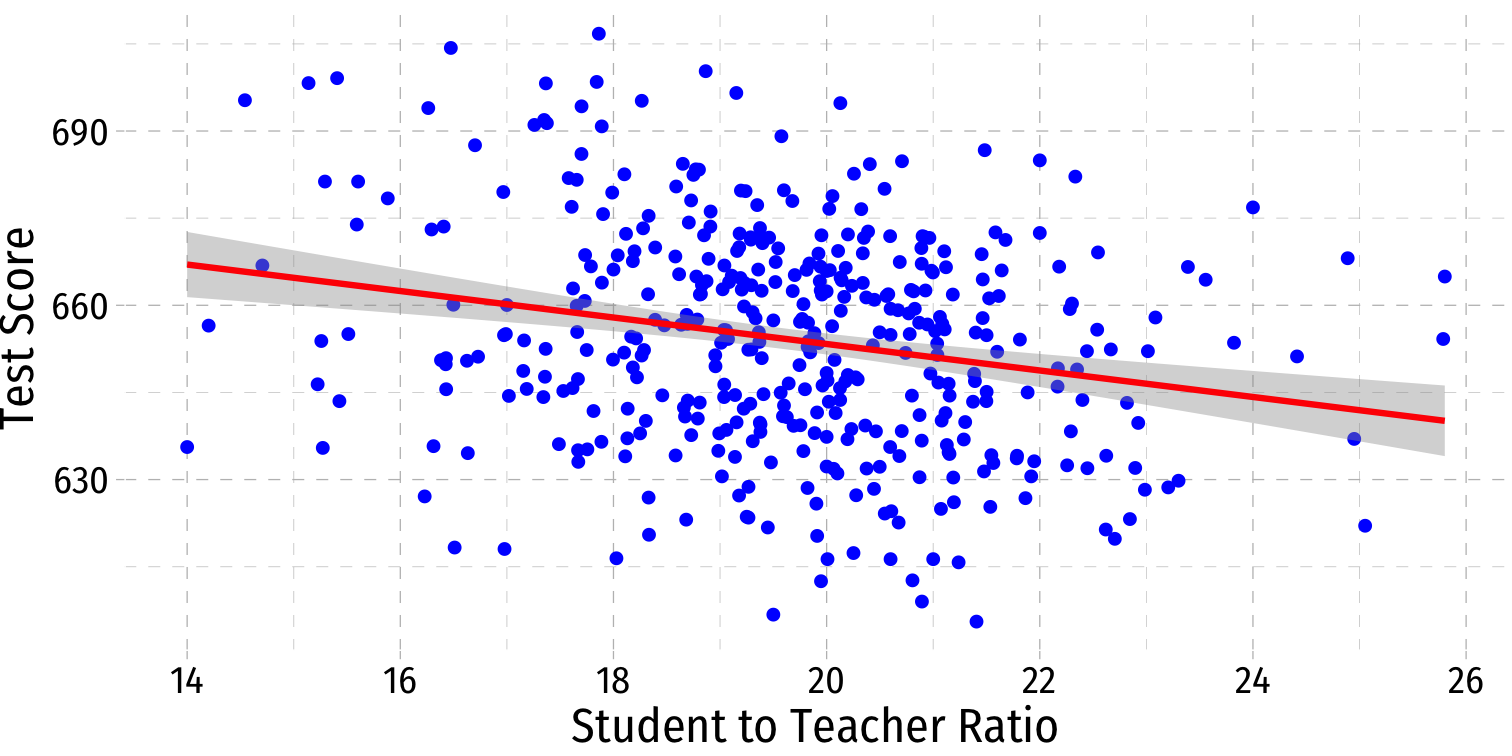
Visualizing Heteroskedasticity I

  • Our original scatterplot with regression line

  • Does the spread of the errors change over different values of str?

    • No: homoskedastic
    • Yes: heteroskedastic

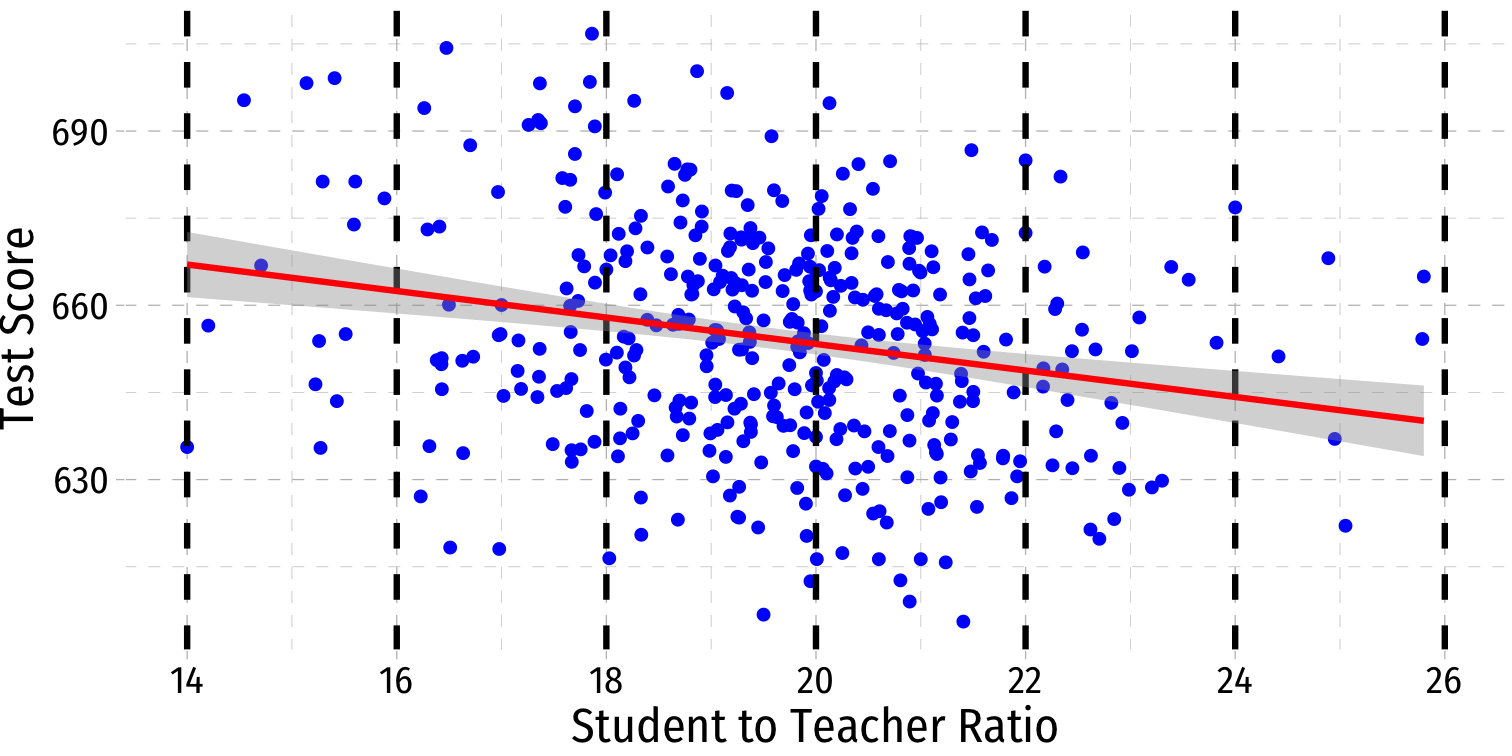
Visualizing Heteroskedasticity I

  • Our original scatterplot with regression line

  • Does the spread of the errors change over different values of str?

    • No: homoskedastic
    • Yes: heteroskedastic

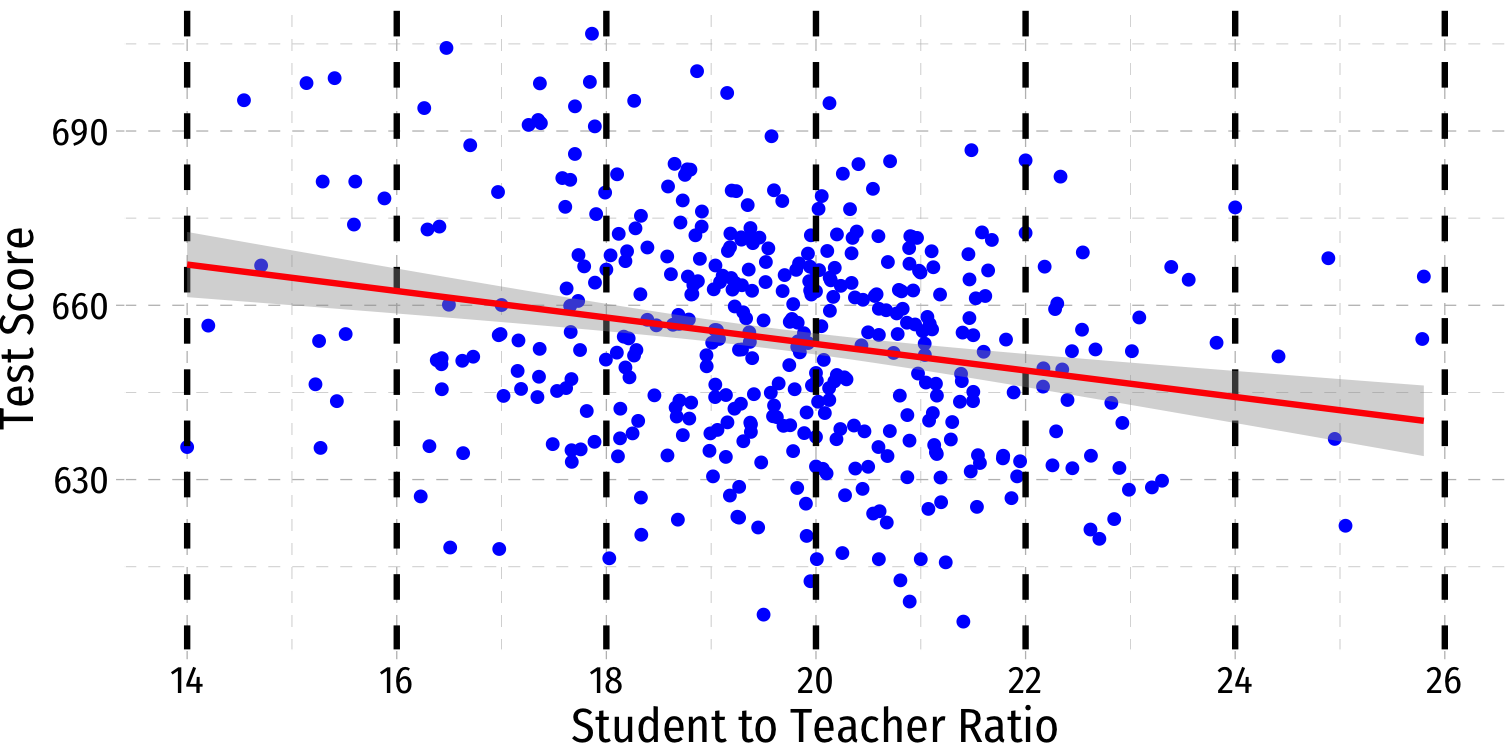
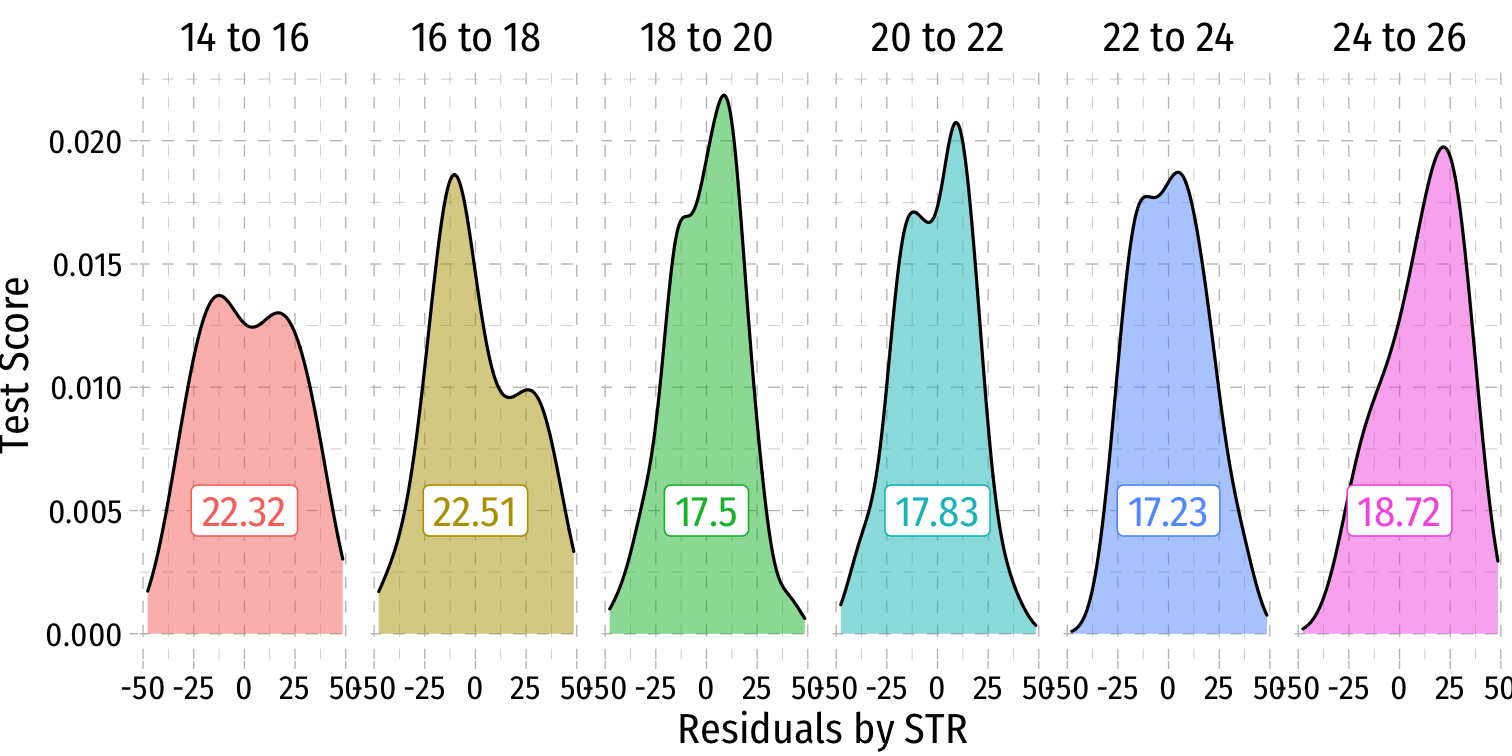
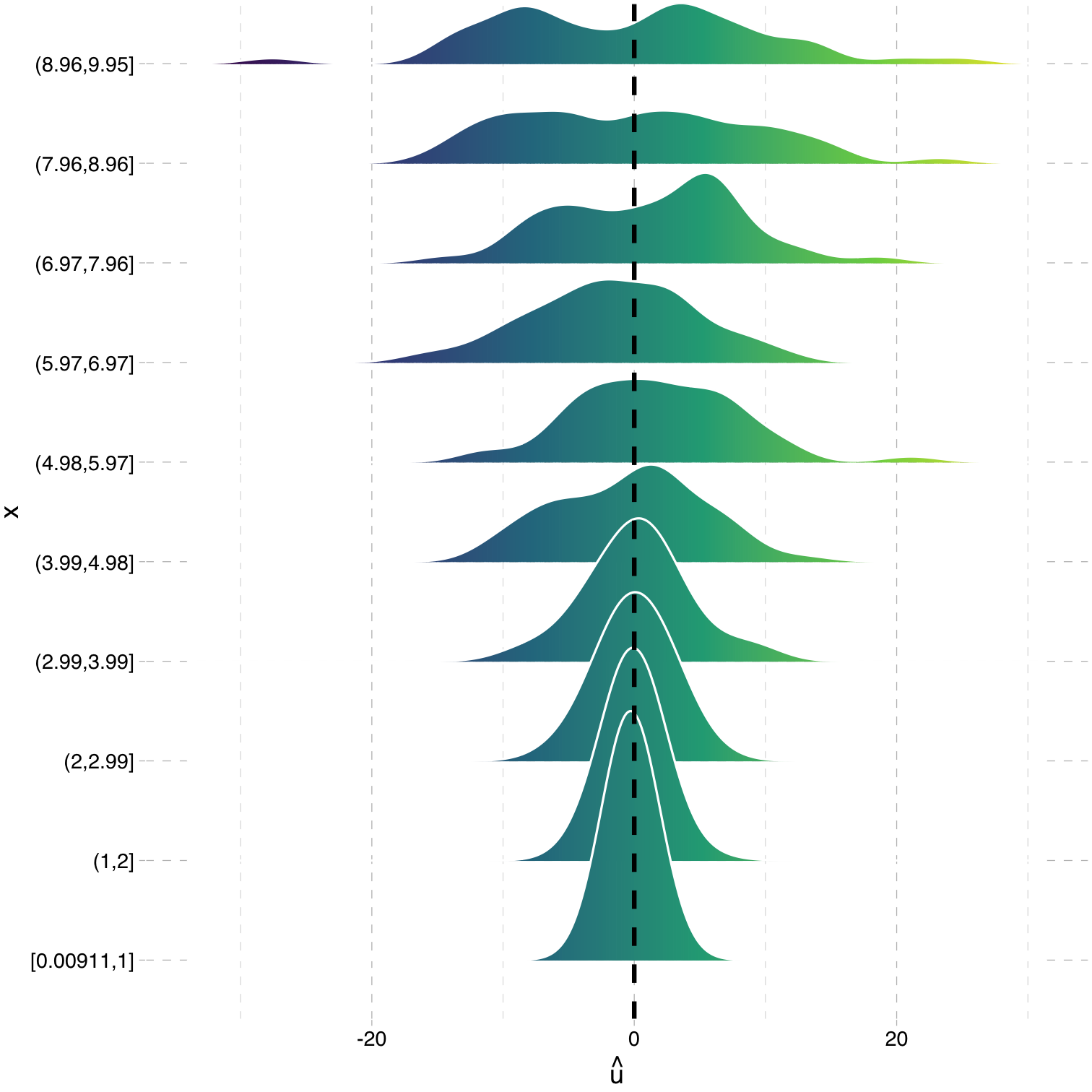
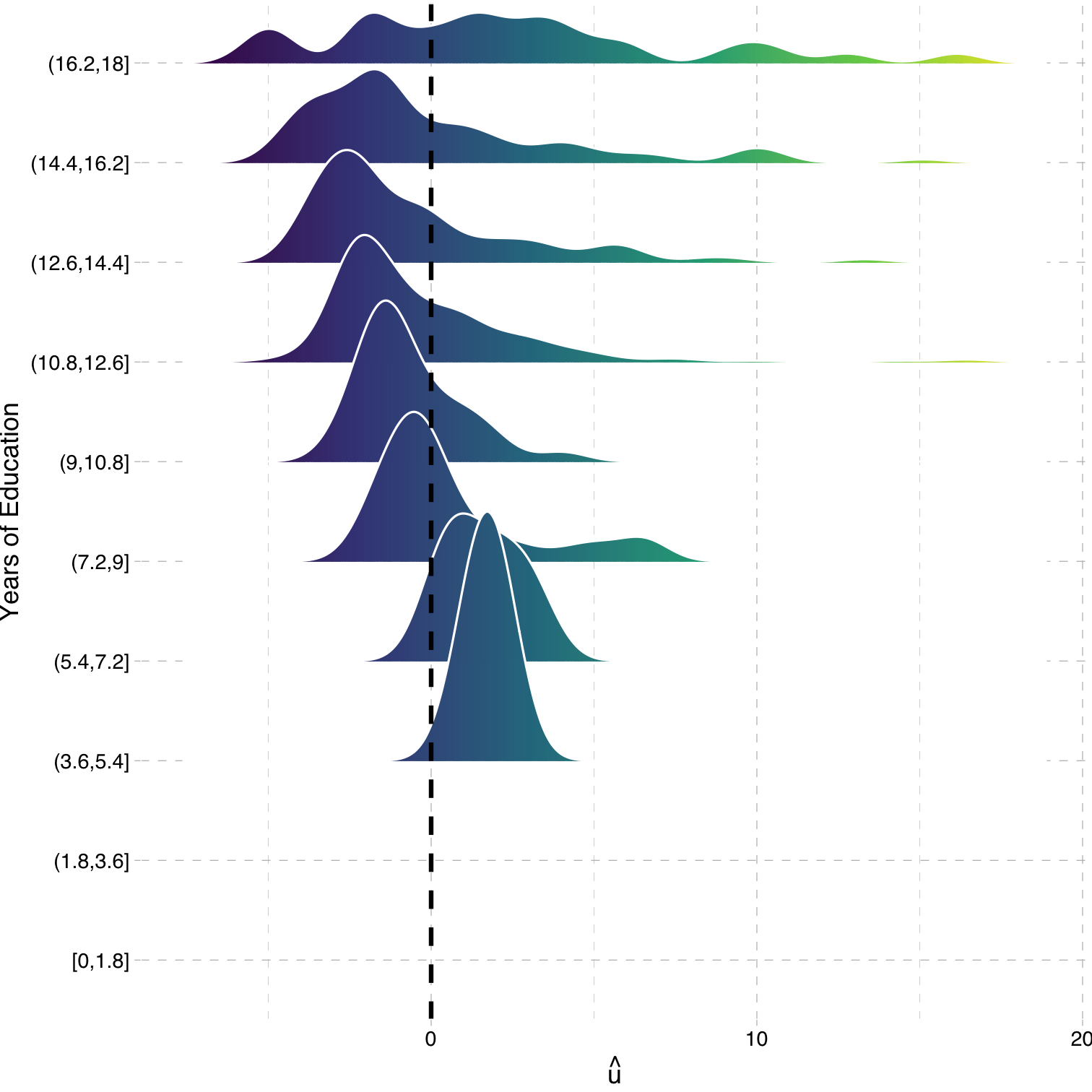
Heteroskedasticity: Another View

  • Using the ggridges package

  • Plotting the (conditional) distribution of errors by STR

  • See that the variation in errors (ˆu) changes across class sizes!

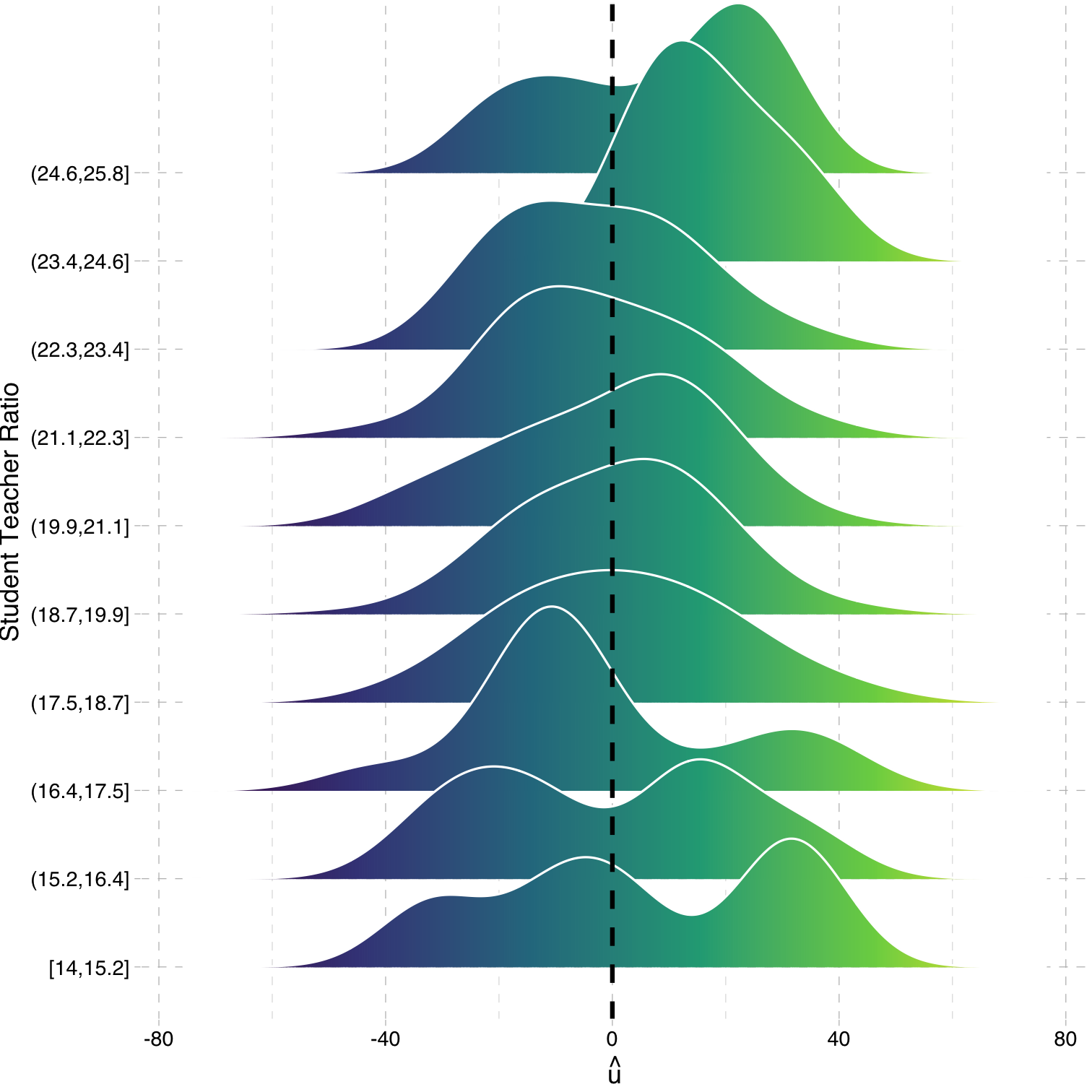
More Obvious Heteroskedasticity

  • Visual cue: data is "fan-shaped"
    • Data points are closer to line in some areas
    • Data points are more spread from line in other areas

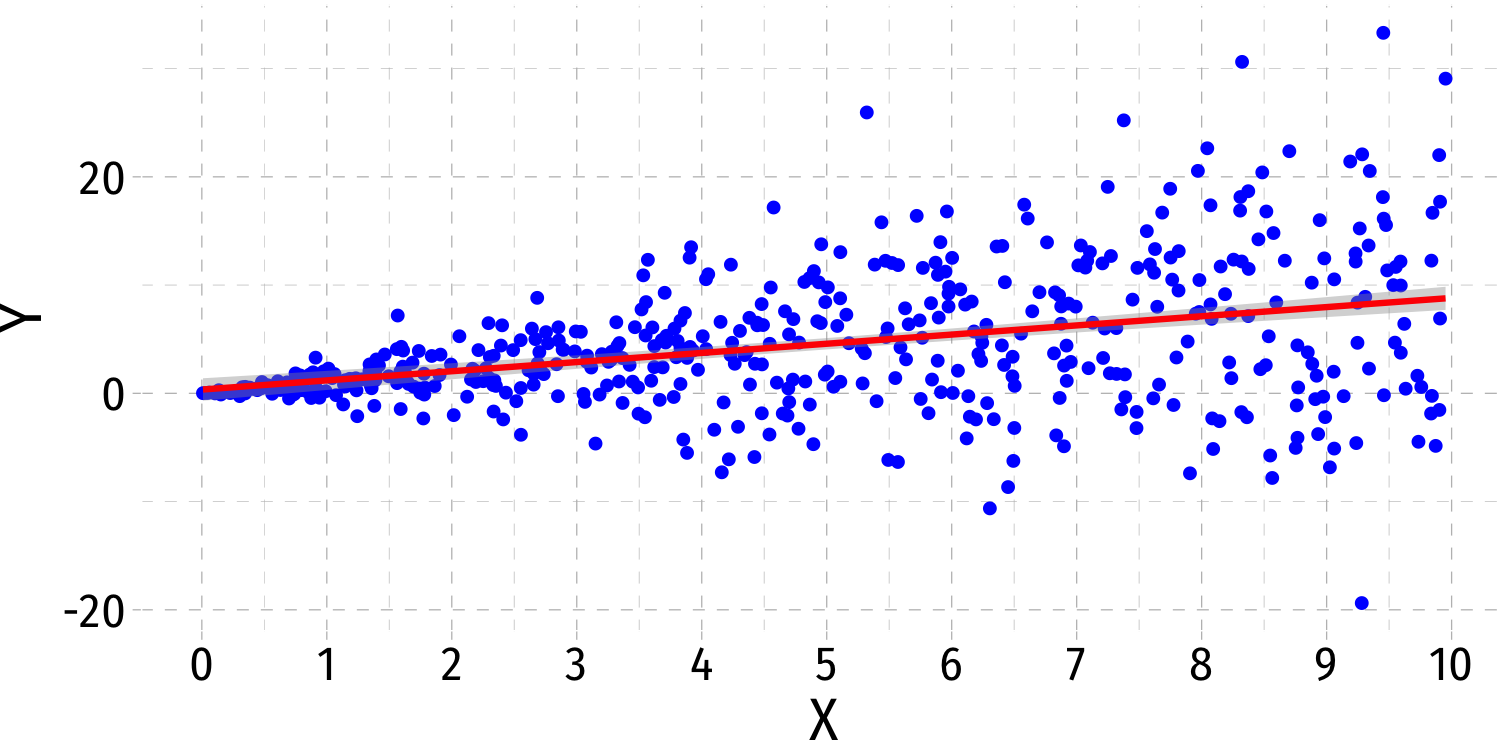
More Obvious Heteroskedasticity

  • Visual cue: data is "fan-shaped"
    • Data points are closer to line in some areas
    • Data points are more spread from line in other areas

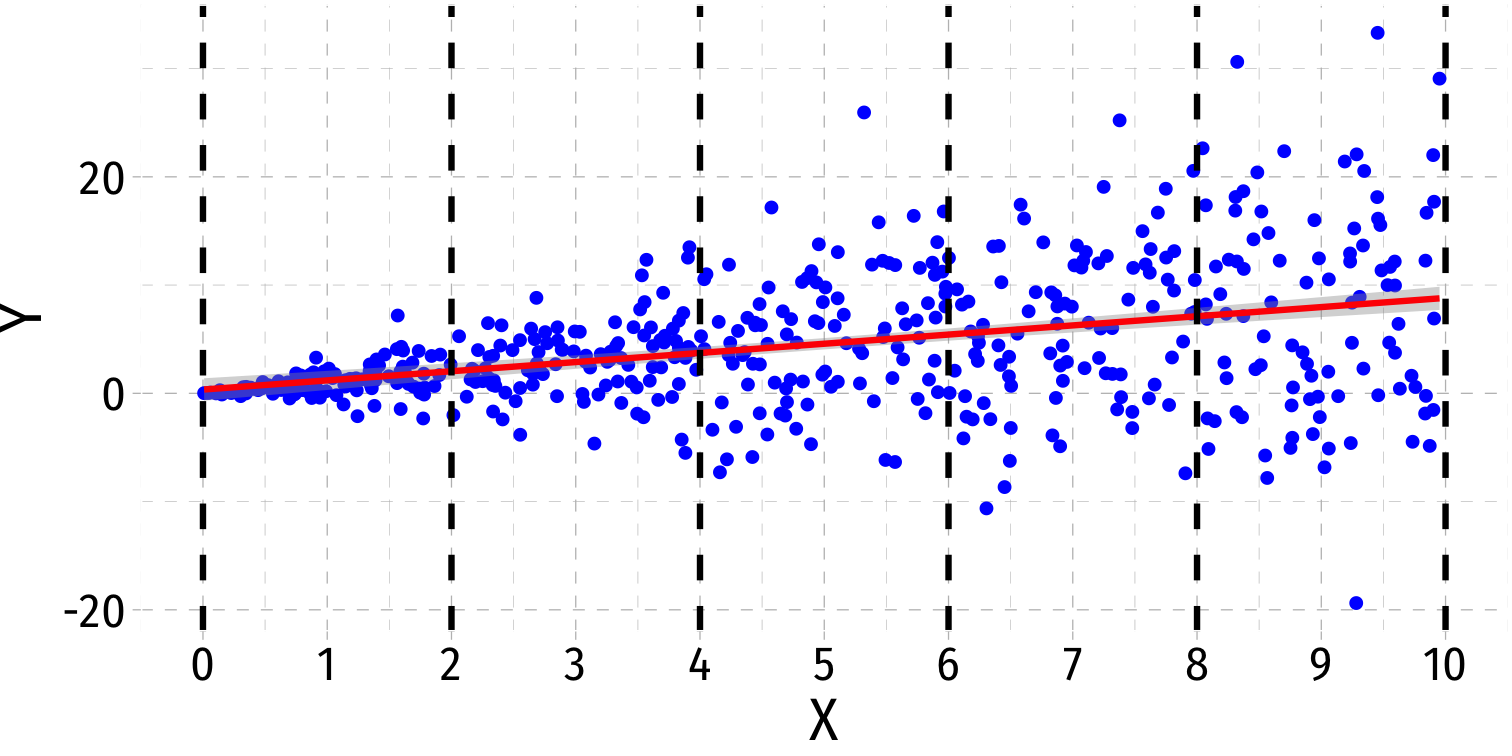
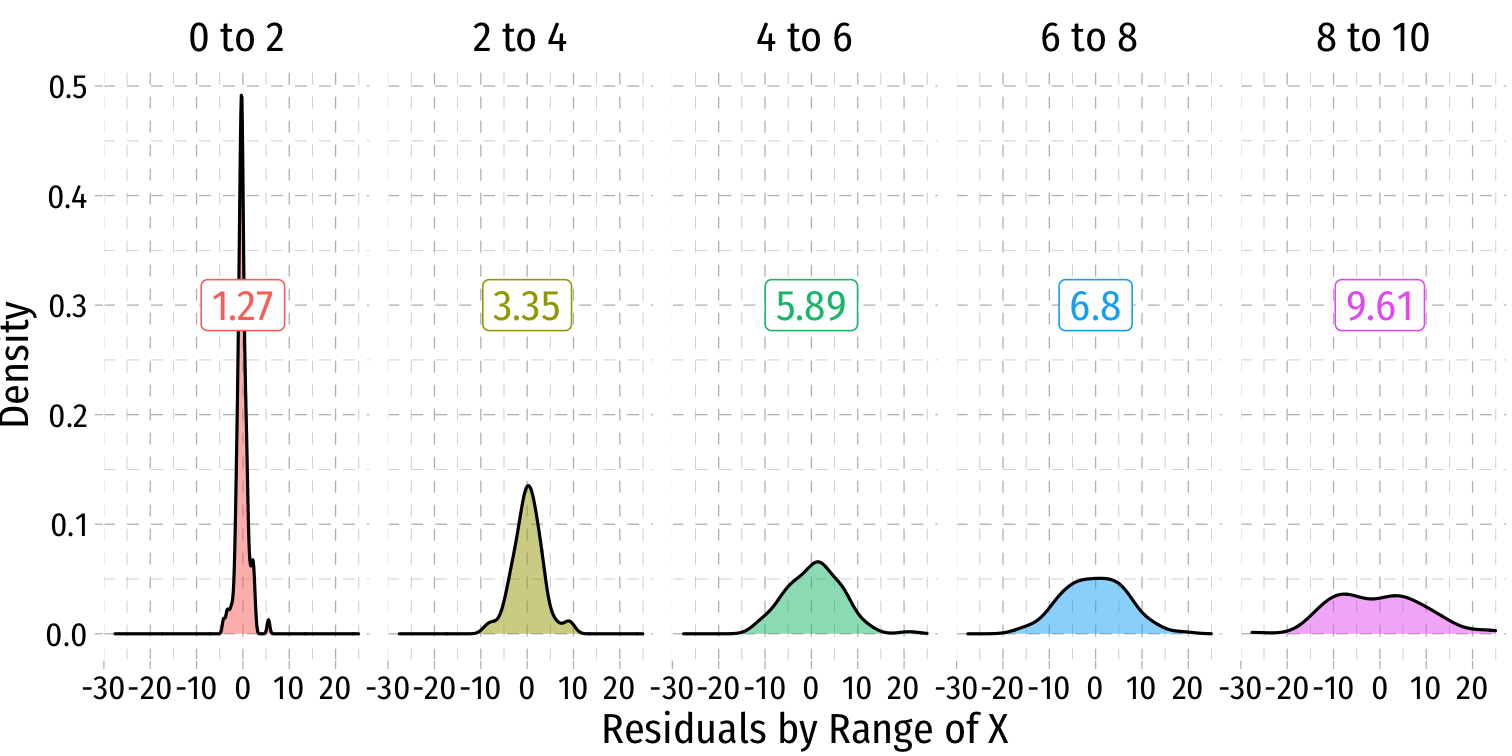
Heteroskedasticity: Another View

  • Using the ggridges package

  • Plotting the (conditional) distribution of errors by x

What Might Cause Heteroskedastic Errors?

^wagei=^β0+^β1educi

Wage
Intercept-0.90    
(0.68)   
Years of Schooling0.54 ***
(0.05)   
N526       
R-Squared0.16    
SER3.38    
*** p < 0.001; ** p < 0.01; * p < 0.05.

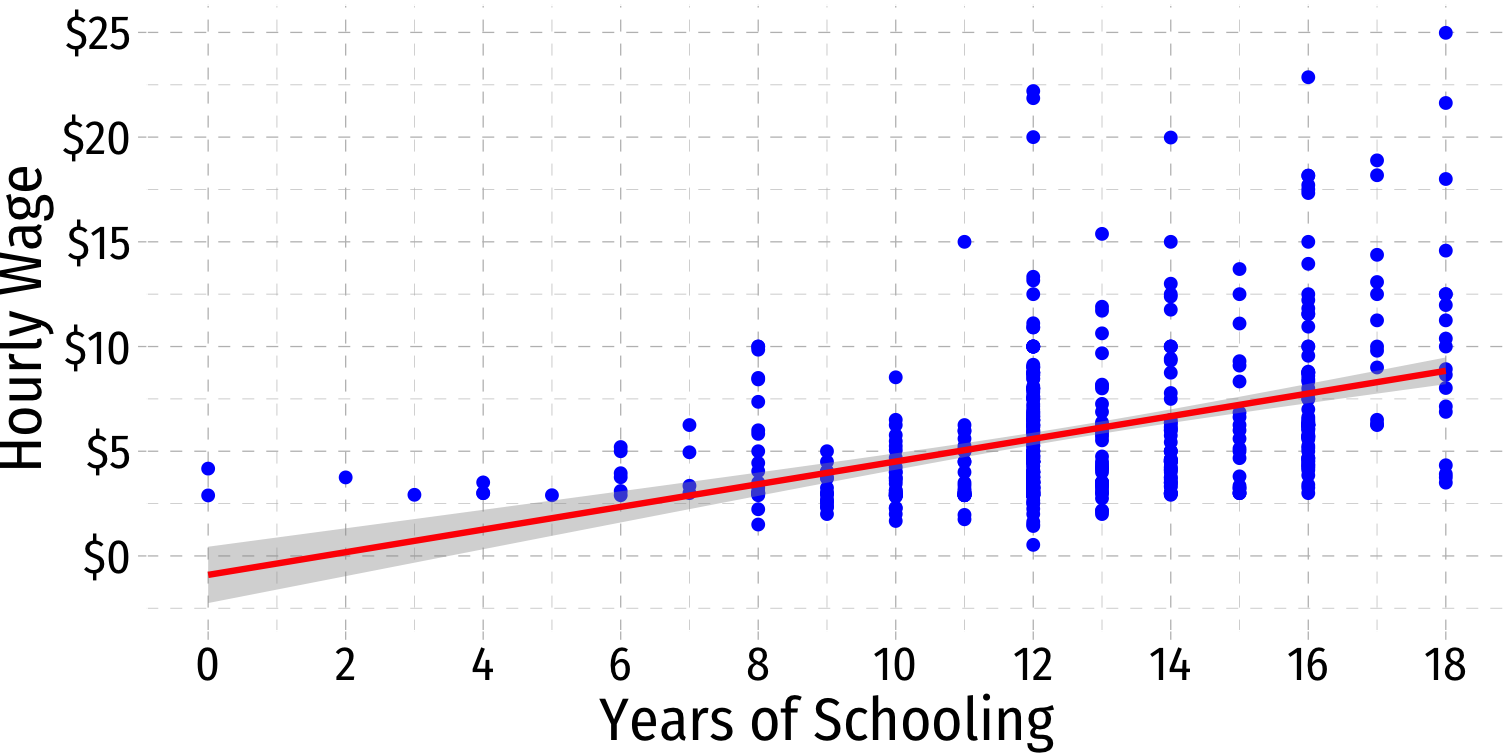
What Might Cause Heteroskedastic Errors?

^wagei=^β0+^β1educi

Wage
Intercept-0.90    
(0.68)   
Years of Schooling0.54 ***
(0.05)   
N526       
R-Squared0.16    
SER3.38    
*** p < 0.001; ** p < 0.01; * p < 0.05.

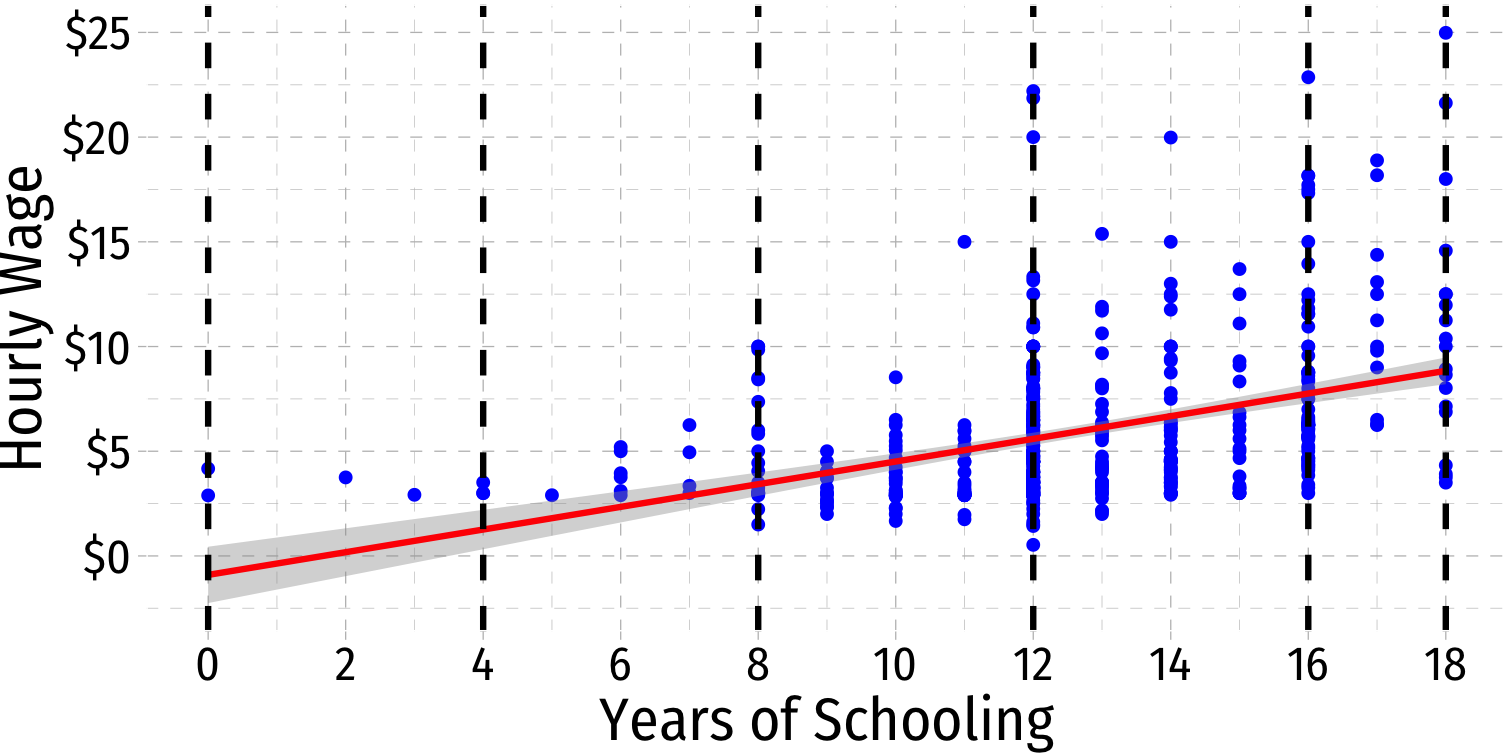
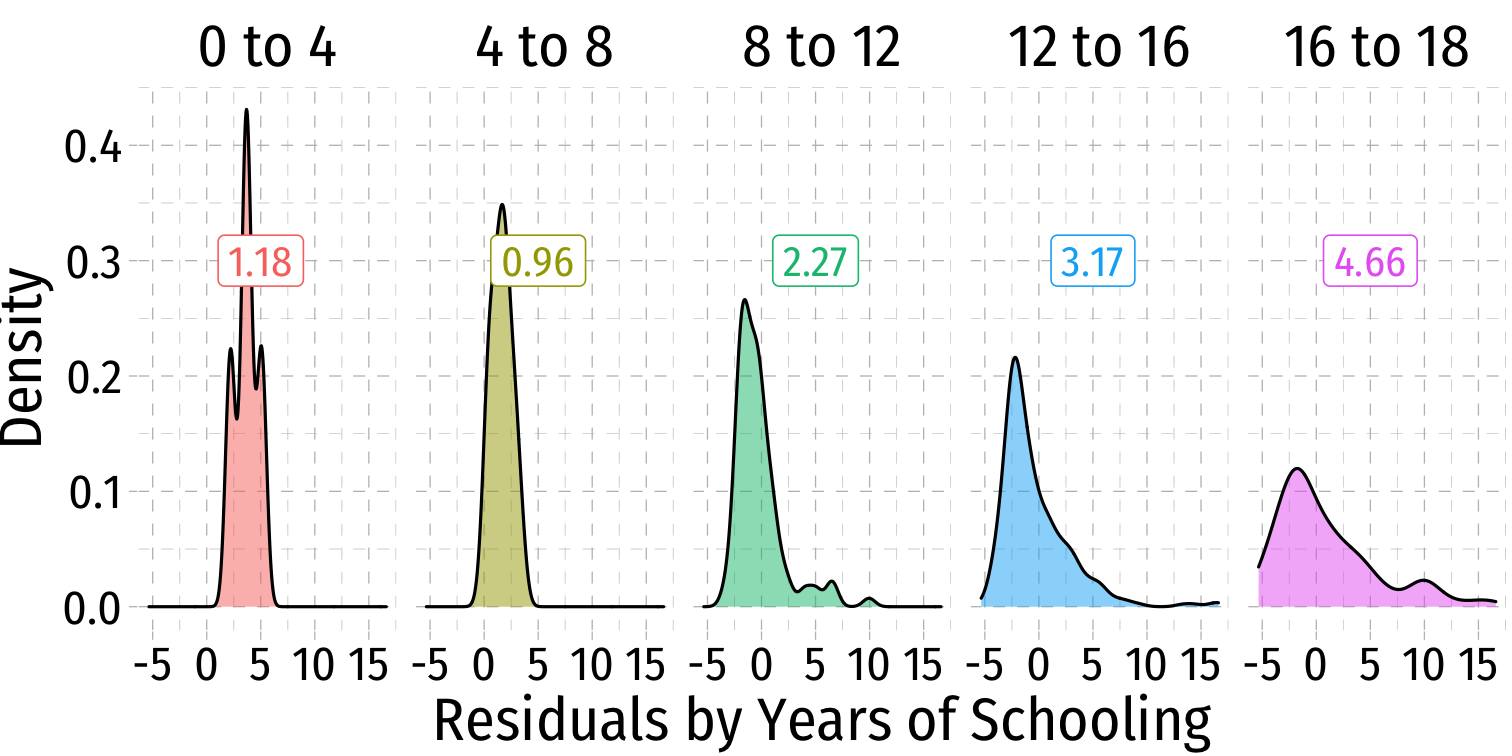
Heteroskedasticity: Another View

  • Using the ggridges package

  • Plotting the (conditional) distribution of errors by education

Detecting Heteroskedasticity I

  • Several tests to check if data is heteroskedastic
  • One common test is Breusch-Pagan test
  • Can use bptest() with lmtest package in R
    • H0: homoskedastic
    • If p-value < 0.05, reject H0⟹ heteroskedastic

Detecting Heteroskedasticity I

  • Several tests to check if data is heteroskedastic
  • One common test is Breusch-Pagan test
  • Can use bptest() with lmtest package in R
    • H0: homoskedastic
    • If p-value < 0.05, reject H0⟹ heteroskedastic
# install.packages("lmtest")
library("lmtest")
bptest(school_reg)
## 
##     studentized Breusch-Pagan test
## 
## data:  school_reg
## BP = 5.7936, df = 1, p-value = 0.01608

Detecting Heteroskedasticity II

  • How about our wage regression?
# install.packages("lmtest")
library("lmtest")
bptest(wage_reg)
## 
##     studentized Breusch-Pagan test
## 
## data:  wage_reg
## BP = 15.306, df = 1, p-value = 9.144e-05

Fixing Heteroskedasticity I

  • Heteroskedasticity is easy to fix with software that can calculate robust standard errors (using the more complicated formula above)

  • Easiest method is to use estimatr package

    • lm_robust() command (instead of lm) to run regression
    • set se_type="stata" to calculate robust SEs using the formula above
#install.packages("estimatr")
library(estimatr)
school_reg_robust <-lm_robust(testscr ~ str, data = CASchool,
                              se_type = "stata")
school_reg_robust
##               Estimate Std. Error   t value      Pr(>|t|)   CI Lower   CI Upper
## (Intercept) 698.932952 10.3643599 67.436191 9.486678e-227 678.560192 719.305713
## str          -2.279808  0.5194892 -4.388557  1.446737e-05  -3.300945  -1.258671
##              DF
## (Intercept) 418
## str         418

Fixing Heteroskedasticity II

library(huxtable)
huxreg("Normal" = school_reg,
       "Robust" = school_reg_robust,
       coefs = c("Intercept" = "(Intercept)",
                 "STR" = "str"),
       statistics = c("N" = "nobs",
                      "R-Squared" = "r.squared",
                      "SER" = "sigma"),
       number_format = 2)
NormalRobust
Intercept698.93 ***698.93 ***
(9.47)   (10.36)   
STR-2.28 ***-2.28 ***
(0.48)   (0.52)   
N420       420       
R-Squared0.05    0.05    
SER18.58           
*** p < 0.001; ** p < 0.01; * p < 0.05.

Assumption 3: No Serial Correlation

  • Errors are not correlated across observations: cor(ui,uj)=0∀i≠j

  • For simple cross-sectional data, this is rarely an issue

  • Time-series & panel data nearly always contain serial correlation or autocorrelation between errors

  • Errors may be clustered

    • by group: e.g. all observations from Maryland, all observations from Virginia, etc.
    • by time: GDP in 2006 around the world, GDP in 2008 around the world, etc.

  • We'll deal with these fixes when we talk about panel data (or time-series if necessary)

Outliers

Outliers Can Bias OLS! I

  • Outliers can affect the slope (and intercept) of the line and add bias

    • May be result of human error (measurement, transcribing, etc)
    • May be meaningful and accurate

  • In any case, compare how including/dropping outliers affects regression and always discuss outliers!

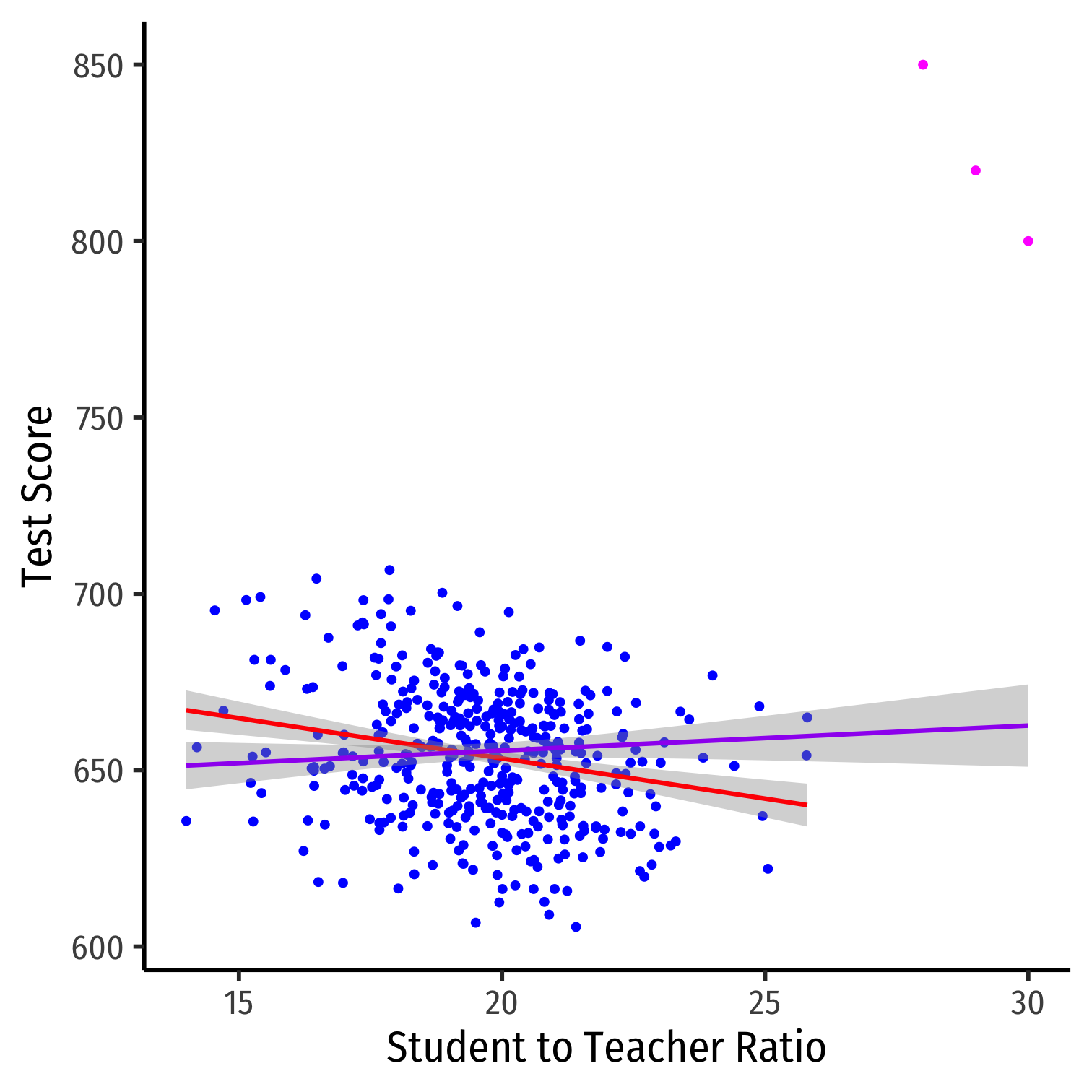
Outliers Can Bias OLS! II

huxreg("No Outliers" = school_reg,
       "Outliers" = school_outlier_reg,
       coefs = c("Intercept" = "(Intercept)",
                 "STR" = "str"),
       statistics = c("N" = "nobs",
                      "R-Squared" = "r.squared",
                      "SER" = "sigma"),
       number_format = 2)
No OutliersOutliers
Intercept698.93 ***641.40 ***
(9.47)   (11.21)   
STR-2.28 ***0.71    
(0.48)   (0.57)   
N420       423       
R-Squared0.05    0.00    
SER18.58    23.76    
*** p < 0.001; ** p < 0.01; * p < 0.05.

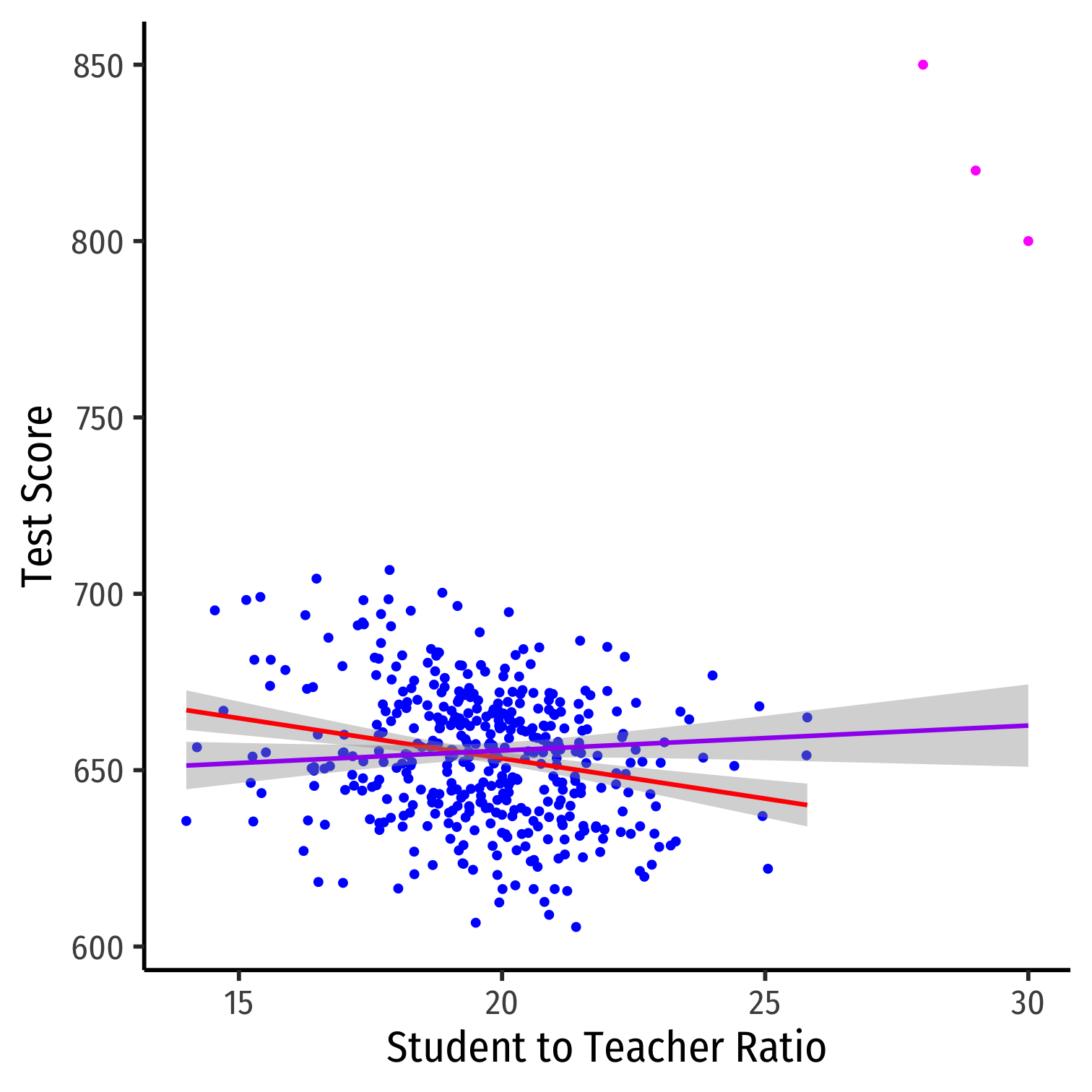
Detecting Outliers

  • The car package has an outlierTest command to run on the regression
library("car")
# Use Bonferonni test 
outlierTest(school_outlier_reg) # will point out which obs #s seem outliers
##     rstudent unadjusted p-value Bonferroni p
## 422 8.822768         3.0261e-17   1.2800e-14
## 423 7.233470         2.2493e-12   9.5147e-10
## 421 6.232045         1.1209e-09   4.7414e-07
# find these observations
CA.outlier %>%
  slice(c(422,423,421))
observatdistricttestscrstr
422Crazy School 285028
423Crazy School 382029
421Crazy School 180030

Outline

Variation in ^β1

Presenting Regression Results

Diagnostics about Regression

Problem: Heteroskedasticity

Outliers

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow