3.7 — Interaction Effects
ECON 480 • Econometrics • Fall 2020
Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsF20
metricsF20.classes.ryansafner.com
Sliders and Switches

Sliders and Switches

Sliders and Switches

- Marginal effect of dummy variable: effect on Y of going from 0 to 1
Sliders and Switches

Marginal effect of dummy variable: effect on Y of going from 0 to 1
Marginal effect of continuous variable: effect on Y of a 1 unit change in X
Interaction Effects
- Sometimes one X variable might interact with another in determining Y
Interaction Effects
- Sometimes one X variable might interact with another in determining Y
Example: Consider the gender pay gap again.
Interaction Effects
- Sometimes one X variable might interact with another in determining Y
Example: Consider the gender pay gap again.
- Gender affects wages
- Experience affects wages
Interaction Effects
- Sometimes one X variable might interact with another in determining Y
Example: Consider the gender pay gap again.
- Gender affects wages
- Experience affects wages
- Does experience affect wages differently by gender?
- i.e. is there an interaction effect between gender and experience?
Interaction Effects
- Sometimes one X variable might interact with another in determining Y
Example: Consider the gender pay gap again.
- Gender affects wages
- Experience affects wages
- Does experience affect wages differently by gender?
- i.e. is there an interaction effect between gender and experience?
- Note this is NOT the same as just asking: “do men earn more than women with the same amount of experience?”
^wagesi=β0+β1Genderi+β2Experiencei
Three Types of Interactions
Depending on the types of variables, there are 3 possible types of interaction effects
We will look at each in turn
Three Types of Interactions
Depending on the types of variables, there are 3 possible types of interaction effects
We will look at each in turn
- Interaction between a dummy and a continuous variable:
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
Three Types of Interactions
Depending on the types of variables, there are 3 possible types of interaction effects
We will look at each in turn
- Interaction between a dummy and a continuous variable:
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
- Interaction between a two dummy variables:
Yi=β0+β1D1i+β2D2i+β3(D1i×D2i)
Three Types of Interactions
Depending on the types of variables, there are 3 possible types of interaction effects
We will look at each in turn
- Interaction between a dummy and a continuous variable:
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
- Interaction between a two dummy variables:
Yi=β0+β1D1i+β2D2i+β3(D1i×D2i)
- Interaction between a two continuous variables:
Yi=β0+β1X1i+β2X2i+β3(X1i×X2i)
Interactions Between a Dummy and Continuous Variable
Interactions: A Dummy & Continuous Variable

Interactions: A Dummy & Continuous Variable

- Does the marginal effect of the continuous variable on Y change depending on whether the dummy is “on” or “off”?
Interactions: A Dummy & Continuous Variable I
- We can model an interaction by introducing a variable that is an interaction term capturing the interaction between two variables:
Yi=β0+β1Xi+β2Di+β3(Xi×Di) where Di={0,1}
Interactions: A Dummy & Continuous Variable I
- We can model an interaction by introducing a variable that is an interaction term capturing the interaction between two variables:
Yi=β0+β1Xi+β2Di+β3(Xi×Di) where Di={0,1}
- β3 estimates the interaction effect between Xi and Di on Yi
Interactions: A Dummy & Continuous Variable I
- We can model an interaction by introducing a variable that is an interaction term capturing the interaction between two variables:
Yi=β0+β1Xi+β2Di+β3(Xi×Di) where Di={0,1}
β3 estimates the interaction effect between Xi and Di on Yi
What do the different coefficients (β)’s tell us?
- Again, think logically by examining each group (Di=0 or Di=1)
Interaction Effects as Two Regressions I
Yi=β0+β1Xi+β2Di+β3Xi×Di
Interaction Effects as Two Regressions I
Yi=β0+β1Xi+β2Di+β3Xi×Di
- When Di=0 (Control group):
^Yi=^β0+^β1Xi+^β2(0)+^β3Xi×(0)^Yi=^β0+^β1Xi
Interaction Effects as Two Regressions I
Yi=β0+β1Xi+β2Di+β3Xi×Di
- When Di=0 (Control group):
^Yi=^β0+^β1Xi+^β2(0)+^β3Xi×(0)^Yi=^β0+^β1Xi
- When Di=1 (Treatment group):
^Yi=^β0+^β1Xi+^β2(1)+^β3Xi×(1)^Yi=(^β0+^β2)+(^β1+^β3)Xi
Interaction Effects as Two Regressions I
Yi=β0+β1Xi+β2Di+β3Xi×Di
- When Di=0 (Control group):
^Yi=^β0+^β1Xi+^β2(0)+^β3Xi×(0)^Yi=^β0+^β1Xi
- When Di=1 (Treatment group):
^Yi=^β0+^β1Xi+^β2(1)+^β3Xi×(1)^Yi=(^β0+^β2)+(^β1+^β3)Xi
- So what we really have is two regression lines!
Interaction Effects as Two Regressions II
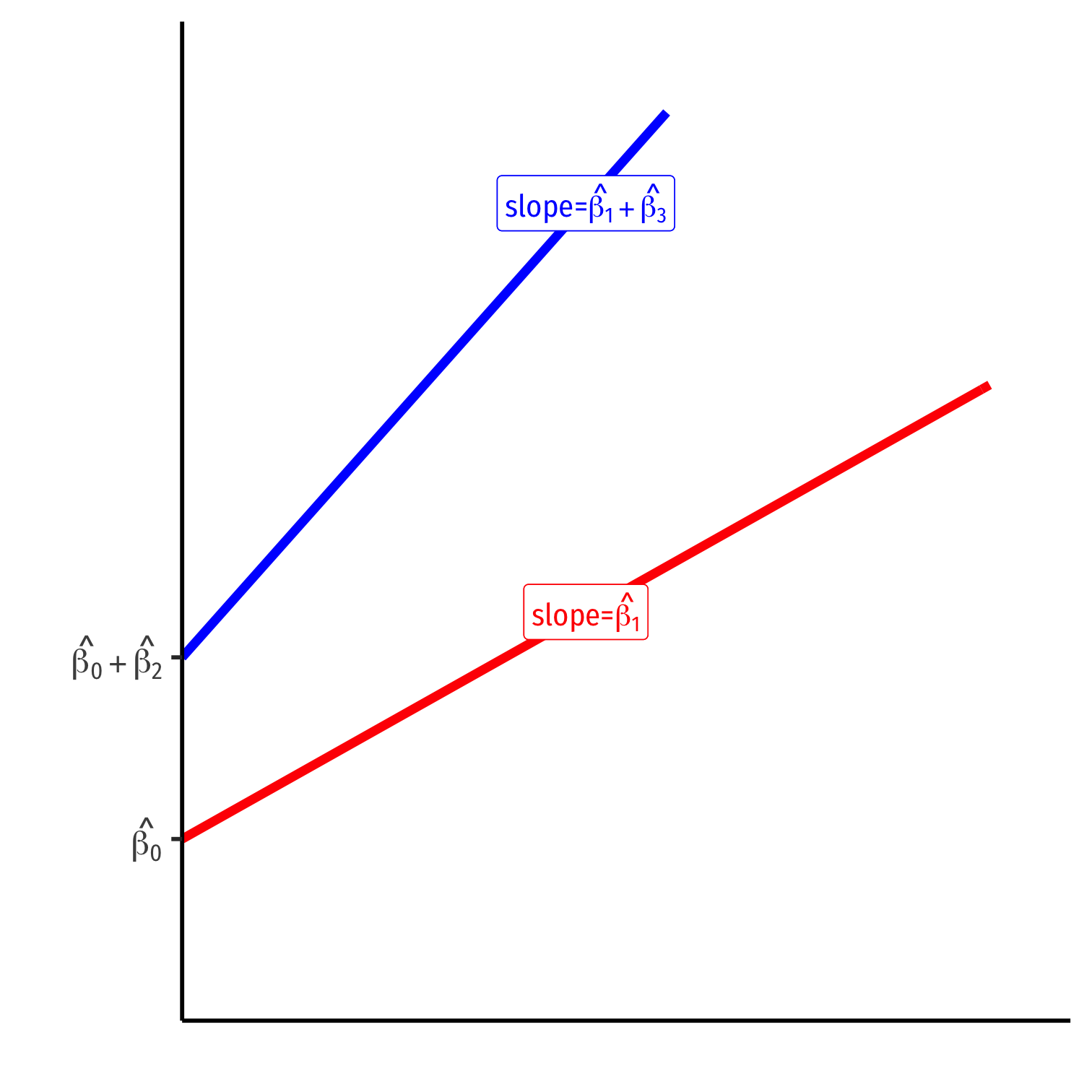
- Di=0 group:
Yi=^β0+^β1Xi
- Di=1 group:
Yi=(^β0+^β2)+(^β1+^β3)Xi
Interpretting Coefficients I
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
- To interpret the coefficients, compare cases after changing X by ΔX:
Interpretting Coefficients I
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
- To interpret the coefficients, compare cases after changing X by ΔX:
Yi+ΔYi=β0+β1(Xi+ΔXi)β2Di+β3((Xi+ΔXi)Di)
Interpretting Coefficients I
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
- To interpret the coefficients, compare cases after changing X by ΔX:
Yi+ΔYi=β0+β1(Xi+ΔXi)β2Di+β3((Xi+ΔXi)Di)
- Subtracting these two equations, the difference is:
Interpretting Coefficients I
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
- To interpret the coefficients, compare cases after changing X by ΔX:
Yi+ΔYi=β0+β1(Xi+ΔXi)β2Di+β3((Xi+ΔXi)Di)
- Subtracting these two equations, the difference is:
ΔYi=β1ΔXi+β3DiΔXiΔYiΔXi=β1+β3Di
Interpretting Coefficients I
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
- To interpret the coefficients, compare cases after changing X by ΔX:
Yi+ΔYi=β0+β1(Xi+ΔXi)β2Di+β3((Xi+ΔXi)Di)
- Subtracting these two equations, the difference is:
ΔYi=β1ΔXi+β3DiΔXiΔYiΔXi=β1+β3Di
The effect of X→Y depends on the value of Di!
β3: increment to the effect of X→Y when Di=1 (vs. Di=0)
Interpretting Coefficients II
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
- ^β0: E[Yi] for Xi=0 and Di=0
Interpretting Coefficients II
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
^β0: E[Yi] for Xi=0 and Di=0
β1: Marginal effect of Xi→Yi for Di=0
Interpretting Coefficients II
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
^β0: E[Yi] for Xi=0 and Di=0
β1: Marginal effect of Xi→Yi for Di=0
β2: Marginal effect on Yi of difference between Di=0 and Di=1
Interpretting Coefficients II
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
^β0: E[Yi] for Xi=0 and Di=0
β1: Marginal effect of Xi→Yi for Di=0
β2: Marginal effect on Yi of difference between Di=0 and Di=1
β3: The difference of the marginal effect of Xi→Yi between Di=0 and Di=1
Interpretting Coefficients II
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
^β0: E[Yi] for Xi=0 and Di=0
β1: Marginal effect of Xi→Yi for Di=0
β2: Marginal effect on Yi of difference between Di=0 and Di=1
β3: The difference of the marginal effect of Xi→Yi between Di=0 and Di=1
This is a bit awkward, easier to think about the two regression lines:
Interpretting Coefficients III
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
Interpretting Coefficients III
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
For Di=0 Group: ^Yi=^β0+^β1Xi
- Intercept: ^β0
- Slope: ^β1
Interpretting Coefficients III
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
For Di=0 Group: ^Yi=^β0+^β1Xi
- Intercept: ^β0
- Slope: ^β1
For Di=1 Group: ^Yi=(^β0+^β2)+(^β1+^β3)Xi
- Intercept: ^β0+^β2
- Slope: ^β1+^β3
Interpretting Coefficients III
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
For Di=0 Group: ^Yi=^β0+^β1Xi
- Intercept: ^β0
- Slope: ^β1
For Di=1 Group: ^Yi=(^β0+^β2)+(^β1+^β3)Xi
- Intercept: ^β0+^β2
- Slope: ^β1+^β3
^β2: difference in intercept between groups
^β3: difference in slope between groups
Interpretting Coefficients III
Yi=β0+β1Xi+β2Di+β3(Xi×Di)
For Di=0 Group: ^Yi=^β0+^β1Xi
- Intercept: ^β0
- Slope: ^β1
For Di=1 Group: ^Yi=(^β0+^β2)+(^β1+^β3)Xi
- Intercept: ^β0+^β2
- Slope: ^β1+^β3
^β2: difference in intercept between groups
^β3: difference in slope between groups
- How can we determine if the two lines have the same slope and/or intercept?
- Same intercept? t-test H0: β2=0
- Same slope? t-test H0: β3=0
Example I
Example: ^wagei=^β0+^β1experi+^β2femalei+^β3(experi×femalei)
Example I
Example: ^wagei=^β0+^β1experi+^β2femalei+^β3(experi×femalei)
- For males (female=0):
^wagei=^β0+^β1exper
Example I
Example: ^wagei=^β0+^β1experi+^β2femalei+^β3(experi×femalei)
For males (female=0): ^wagei=^β0+^β1exper
For females (female=1): ^wagei=(^β0+^β2)⏟intercept+(^β1+^β3)⏟slopeexper
Example II
interaction_plot <- ggplot(data = wages)+ aes(x = exper, y = wage, color = as.factor(Gender))+ # make factor geom_point(alpha = 0.5)+ scale_y_continuous(labels=scales::dollar)+ labs(x = "Experience (Years)", y = "Wage")+ scale_color_manual(values = c("Female" = "#e64173", "Male" = "#0047AB") )+ # setting custom colors guides(color=F)+ # hide legend theme_slidesinteraction_plot- Need to make sure
coloraesthetic uses afactorvariable- Can just use
as.factor()in ggplot code
- Can just use
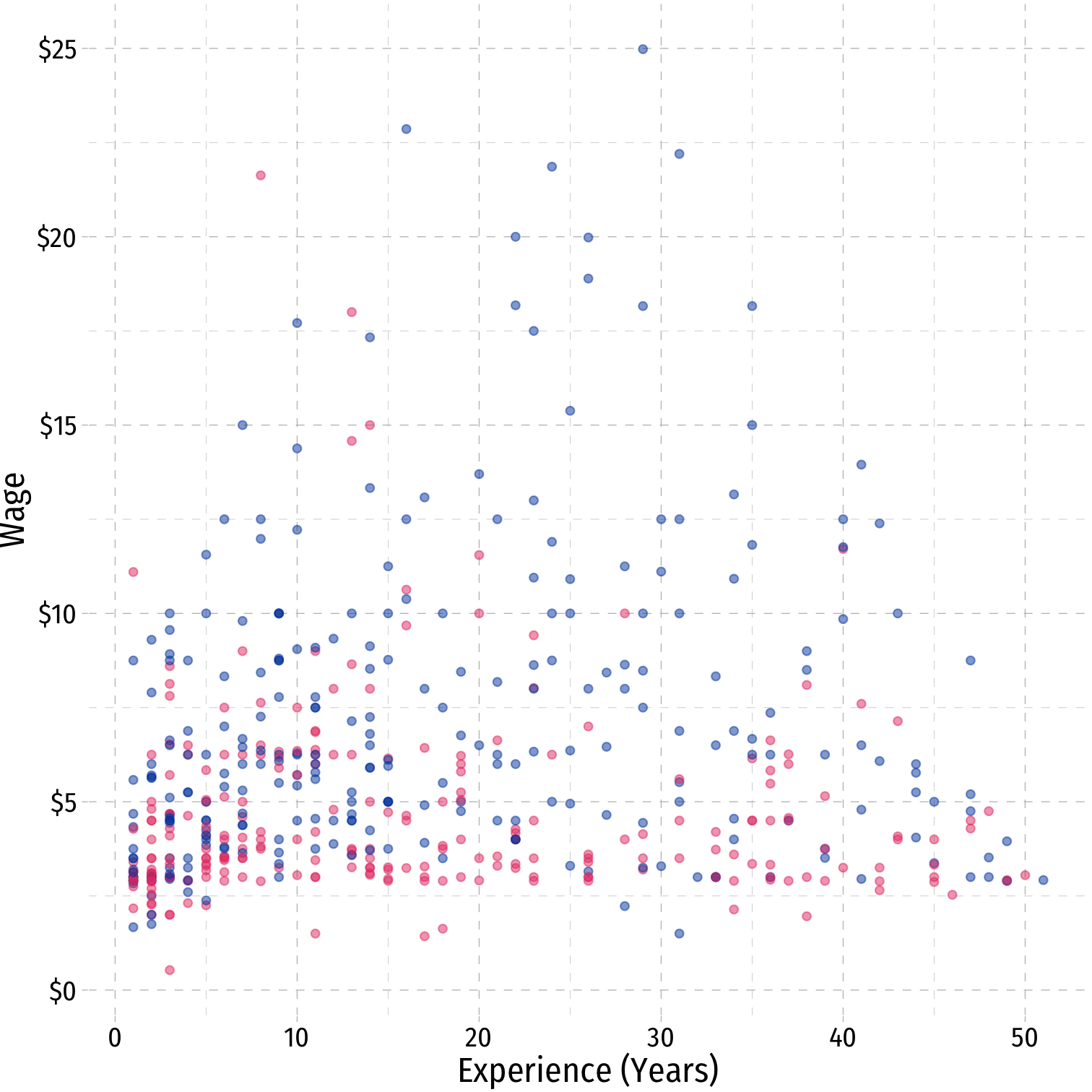
Example II
interaction_plot+ geom_smooth(method="lm")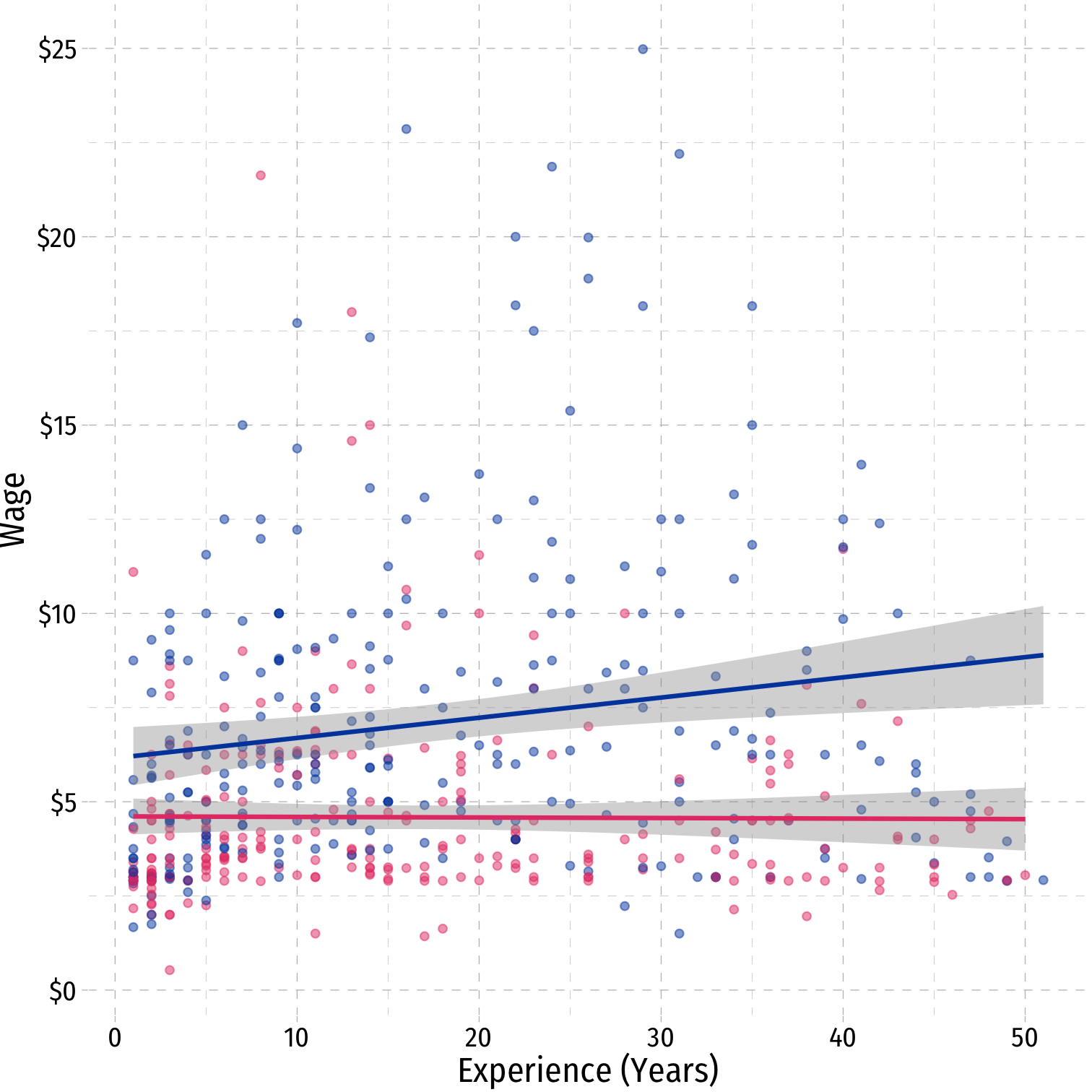
Example II
interaction_plot+ geom_smooth(method="lm")+ facet_wrap(~Gender)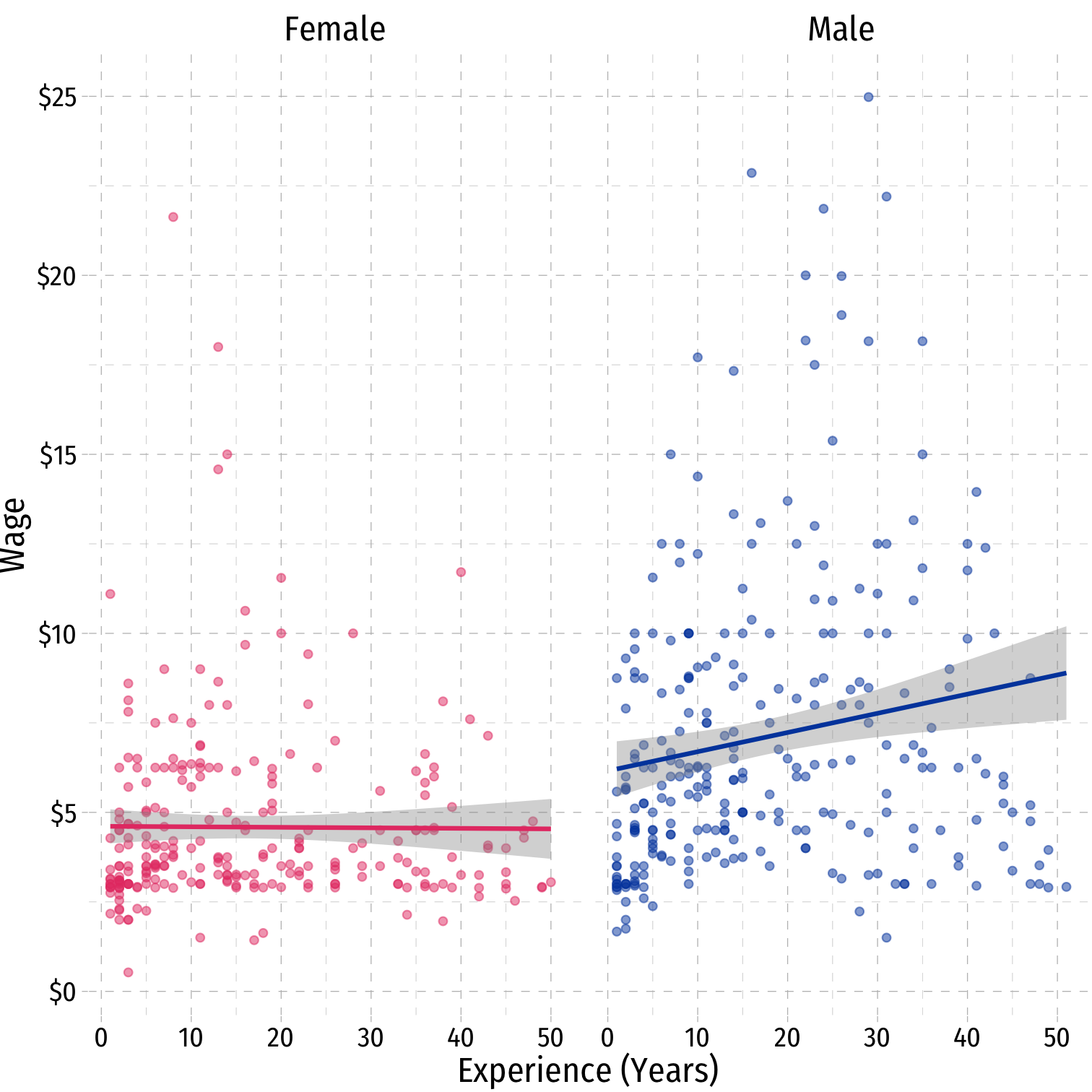
Example Regression in R I
- Syntax for adding an interaction term is easy in
R:var1 * var2- Or could just do
var1 * var2(multiply)
- Or could just do
# both are identical in Rinteraction_reg <- lm(wage ~ exper * female, data = wages)interaction_reg <- lm(wage ~ exper + female + exper * female, data = wages)| ABCDEFGHIJ0123456789 |
term <chr> | estimate <dbl> | std.error <dbl> | statistic <dbl> | p.value <dbl> |
|---|---|---|---|---|
| (Intercept) | 6.15827549 | 0.34167408 | 18.023830 | 7.998534e-57 |
| exper | 0.05360476 | 0.01543716 | 3.472450 | 5.585255e-04 |
| female | -1.54654677 | 0.48186030 | -3.209534 | 1.411253e-03 |
| exper:female | -0.05506989 | 0.02217496 | -2.483427 | 1.332533e-02 |
Example Regression in R III
library(huxtable)huxreg(interaction_reg, coefs = c("Constant" = "(Intercept)", "Experience" = "exper", "Female" = "female", "Experience * Female" = "exper:female"), statistics = c("N" = "nobs", "R-Squared" = "r.squared", "SER" = "sigma"), number_format = 2)| (1) | |
|---|---|
| Constant | 6.16 *** |
| (0.34) | |
| Experience | 0.05 *** |
| (0.02) | |
| Female | -1.55 ** |
| (0.48) | |
| Experience * Female | -0.06 * |
| (0.02) | |
| N | 526 |
| R-Squared | 0.14 |
| SER | 3.44 |
| *** p < 0.001; ** p < 0.01; * p < 0.05. | |
Example Regression in R: Interpretting Coefficients
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
Example Regression in R: Interpretting Coefficients
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
- ^β0:
Example Regression in R: Interpretting Coefficients
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
- ^β0: Men with 0 years of experience earn 6.16
Example Regression in R: Interpretting Coefficients
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
^β0: Men with 0 years of experience earn 6.16
^β1:
Example Regression in R: Interpretting Coefficients
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
^β0: Men with 0 years of experience earn 6.16
^β1: For every additional year of experience, men earn $0.05
Example Regression in R: Interpretting Coefficients
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
^β0: Men with 0 years of experience earn 6.16
^β1: For every additional year of experience, men earn $0.05
^β2:
Example Regression in R: Interpretting Coefficients
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
^β0: Men with 0 years of experience earn 6.16
^β1: For every additional year of experience, men earn $0.05
^β2: Women with 0 years of experience earn $1.55 less than men
Example Regression in R: Interpretting Coefficients
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
^β0: Men with 0 years of experience earn 6.16
^β1: For every additional year of experience, men earn $0.05
^β2: Women with 0 years of experience earn $1.55 less than men
^β3:
Example Regression in R: Interpretting Coefficients
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
^β0: Men with 0 years of experience earn 6.16
^β1: For every additional year of experience, men earn $0.05
^β2: Women with 0 years of experience earn $1.55 less than men
^β3: Women earn $0.06 less than men for every additional year of experience
Interpretting Coefficients as 2 Regressions I
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
Interpretting Coefficients as 2 Regressions I
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
Regression for men (female=0) ^wagei=6.16+0.05Experiencei
Interpretting Coefficients as 2 Regressions I
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
Regression for men (female=0) ^wagei=6.16+0.05Experiencei
- Men with 0 years of experience earn $6.16 on average
Interpretting Coefficients as 2 Regressions I
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
Regression for men (female=0) ^wagei=6.16+0.05Experiencei
Men with 0 years of experience earn $6.16 on average
For every additional year of experience, men earn $0.05 more on average
Interpretting Coefficients as 2 Regressions II
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
Regression for women (female=1) ^wagei=6.16+0.05Experiencei−1.55(1)−0.06Experiencei×(1)=(6.16−1.55)+(0.05−0.06)Experiencei=4.61−0.01Experiencei
Interpretting Coefficients as 2 Regressions II
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
Regression for women (female=1) ^wagei=6.16+0.05Experiencei−1.55(1)−0.06Experiencei×(1)=(6.16−1.55)+(0.05−0.06)Experiencei=4.61−0.01Experiencei
- Women with 0 years of experience earn $4.61 on average
Interpretting Coefficients as 2 Regressions II
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
Regression for women (female=1) ^wagei=6.16+0.05Experiencei−1.55(1)−0.06Experiencei×(1)=(6.16−1.55)+(0.05−0.06)Experiencei=4.61−0.01Experiencei
Women with 0 years of experience earn $4.61 on average
For every additional year of experience, women earn $0.01 less on average
Example Regression in R: Hypothesis Testing
- Are slopes & intercepts of the 2 regressions statistically significantly different?
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 6.16 | 0.342 | 18 | 8e-57 |
| exper | 0.0536 | 0.0154 | 3.47 | 0.000559 |
| female | -1.55 | 0.482 | -3.21 | 0.00141 |
| exper:female | -0.0551 | 0.0222 | -2.48 | 0.0133 |
Example Regression in R: Hypothesis Testing
Are slopes & intercepts of the 2 regressions statistically significantly different?
Are intercepts different? H0:β2=0
- Difference between men vs. women for no experience?
- Is ^β2 significant?
- Yes (reject) H0: t=−3.210, p-value = 0.00
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 6.16 | 0.342 | 18 | 8e-57 |
| exper | 0.0536 | 0.0154 | 3.47 | 0.000559 |
| female | -1.55 | 0.482 | -3.21 | 0.00141 |
| exper:female | -0.0551 | 0.0222 | -2.48 | 0.0133 |
Example Regression in R: Hypothesis Testing
Are slopes & intercepts of the 2 regressions statistically significantly different?
Are intercepts different? H0:β2=0
- Difference between men vs. women for no experience?
- Is ^β2 significant?
- Yes (reject) H0: t=−3.210, p-value = 0.00
Are slopes different? H0:β3=0
- Difference between men vs. women for marginal effect of experience?
- Is ^β3 significant?
- Yes (reject) H0: t=−2.48, p-value = 0.01
^wagei=6.16+0.05Experiencei−1.55Femalei−0.06(Experiencei×Femalei)
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 6.16 | 0.342 | 18 | 8e-57 |
| exper | 0.0536 | 0.0154 | 3.47 | 0.000559 |
| female | -1.55 | 0.482 | -3.21 | 0.00141 |
| exper:female | -0.0551 | 0.0222 | -2.48 | 0.0133 |
Interactions Between Two Dummy Variables
Interactions Between Two Dummy Variables

Interactions Between Two Dummy Variables

- Does the marginal effect on Y of one dummy going from “off” to “on” change depending on whether the other dummy is “off” or “on”?
Interactions Between Two Dummy Variables
Yi=β0+β1D1i+β2D2i+β3(D1i×D2i)
- D1i and D2i are dummy variables
Interactions Between Two Dummy Variables
Yi=β0+β1D1i+β2D2i+β3(D1i×D2i)
D1i and D2i are dummy variables
^β1: effect on Y of going from D1i=0 to D1i=1 when D2i=0
Interactions Between Two Dummy Variables
Yi=β0+β1D1i+β2D2i+β3(D1i×D2i)
D1i and D2i are dummy variables
^β1: effect on Y of going from D1i=0 to D1i=1 when D2i=0
^β2: effect on Y of going from D2i=0 to D2i=1 when D1i=0
Interactions Between Two Dummy Variables
Yi=β0+β1D1i+β2D2i+β3(D1i×D2i)
D1i and D2i are dummy variables
^β1: effect on Y of going from D1i=0 to D1i=1 when D2i=0
^β2: effect on Y of going from D2i=0 to D2i=1 when D1i=0
^β3: effect on Y of going from D1i=0 to D1i=1 when D2i=1
- increment to the effect of D1i going from 0 to 1 when D2i=1 (vs. 0)
Interactions Between Two Dummy Variables
Yi=β0+β1D1i+β2D2i+β3(D1i×D2i)
D1i and D2i are dummy variables
^β1: effect on Y of going from D1i=0 to D1i=1 when D2i=0
^β2: effect on Y of going from D2i=0 to D2i=1 when D1i=0
^β3: effect on Y of going from D1i=0 to D1i=1 when D2i=1
- increment to the effect of D1i going from 0 to 1 when D2i=1 (vs. 0)
As always, best to think logically about possibilities (when each dummy =0 or =1)
2 Dummy Interaction: Interpretting Coefficients
Yi=β0+β1D1i+β2D2i+β3(D1i×D2i)
2 Dummy Interaction: Interpretting Coefficients
Yi=β0+β1D1i+β2D2i+β3(D1i×D2i)
- To interpret coefficients, compare cases:
- Hold D2i constant (set to some value D2i=d2)
- Plug in 0s or 1s for D1i
E(Yi|D1i=0,D2i=d2)=β0+β2d2E(Yi|D1i=1,D2i=d2)=β0+β1(1)+β2d2+β3(1)d2
2 Dummy Interaction: Interpretting Coefficients
Yi=β0+β1D1i+β2D2i+β3(D1i×D2i)
- To interpret coefficients, compare cases:
- Hold D2i constant (set to some value D2i=d2)
- Plug in 0s or 1s for D1i
E(Yi|D1i=0,D2i=d2)=β0+β2d2E(Yi|D1i=1,D2i=d2)=β0+β1(1)+β2d2+β3(1)d2
- Subtracting the two, the difference is:
β1+β3d2
- The marginal effect of D1i→Yi depends on the value of D2i
- ^β3 is the increment to the effect of D1 on Y when D2 goes from 0 to 1
Interactions Between 2 Dummy Variables: Example
Example: Does the gender pay gap change if a person is married vs. single?
^wagei=^β0+^β1femalei+^β2marriedi+^β3(femalei×marriedi)
Interactions Between 2 Dummy Variables: Example
Example: Does the gender pay gap change if a person is married vs. single?
^wagei=^β0+^β1femalei+^β2marriedi+^β3(femalei×marriedi)
- Logically, there are 4 possible combinations of femalei={0,1} and marriedi={0,1}
Interactions Between 2 Dummy Variables: Example
Example: Does the gender pay gap change if a person is married vs. single?
^wagei=^β0+^β1femalei+^β2marriedi+^β3(femalei×marriedi)
- Logically, there are 4 possible combinations of femalei={0,1} and marriedi={0,1}
1) Unmarried men (femalei=0,marriedi=0) ^wagei=^β0
Interactions Between 2 Dummy Variables: Example
Example: Does the gender pay gap change if a person is married vs. single?
^wagei=^β0+^β1femalei+^β2marriedi+^β3(femalei×marriedi)
- Logically, there are 4 possible combinations of femalei={0,1} and marriedi={0,1}
1) Unmarried men (femalei=0,marriedi=0) ^wagei=^β0
2) Married men (femalei=0,marriedi=1) ^wagei=^β0+^β2
Interactions Between 2 Dummy Variables: Example
Example: Does the gender pay gap change if a person is married vs. single?
^wagei=^β0+^β1femalei+^β2marriedi+^β3(femalei×marriedi)
- Logically, there are 4 possible combinations of femalei={0,1} and marriedi={0,1}
1) Unmarried men (femalei=0,marriedi=0) ^wagei=^β0
2) Married men (femalei=0,marriedi=1) ^wagei=^β0+^β2
3) Unmarried women (femalei=1,marriedi=0) ^wagei=^β0+^β1
Interactions Between 2 Dummy Variables: Example
Example: Does the gender pay gap change if a person is married vs. single?
^wagei=^β0+^β1femalei+^β2marriedi+^β3(femalei×marriedi)
- Logically, there are 4 possible combinations of femalei={0,1} and marriedi={0,1}
1) Unmarried men (femalei=0,marriedi=0) ^wagei=^β0
2) Married men (femalei=0,marriedi=1) ^wagei=^β0+^β2
3) Unmarried women (femalei=1,marriedi=0) ^wagei=^β0+^β1
4) Married women (femalei=1,marriedi=1) ^wagei=^β0+^β1+^β2+^β3
Looking at the Data
# get average wage for unmarried menwages %>% filter(female == 0, married == 0) %>% summarize(mean = mean(wage))| mean |
|---|
| 5.17 |
# get average wage for married menwages %>% filter(female == 0, married == 1) %>% summarize(mean = mean(wage))| mean |
|---|
| 7.98 |
# get average wage for unmarried womenwages %>% filter(female == 1, married == 0) %>% summarize(mean = mean(wage))| mean |
|---|
| 4.61 |
# get average wage for married womenwages %>% filter(female == 1, married == 1) %>% summarize(mean = mean(wage))| mean |
|---|
| 4.57 |
Two Dummies Interaction: Group Means
^wagei=^β0+^β1femalei+^β2marriedi+^β3(femalei×marriedi)
| Men | Women | |
|---|---|---|
| Unmarried | $5.17 | $4.61 |
| Married | $7.98 | $4.57 |
Interactions Between Two Dummy Variables: In R I
reg_dummies <- lm(wage ~ female + married + female:married, data = wages)reg_dummies %>% tidy()| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 5.17 | 0.361 | 14.3 | 2.26e-39 |
| female | -0.556 | 0.474 | -1.18 | 0.241 |
| married | 2.82 | 0.436 | 6.45 | 2.53e-10 |
| female:married | -2.86 | 0.608 | -4.71 | 3.2e-06 |
Interactions Between Two Dummy Variables: In R II
library(huxtable)huxreg(reg_dummies, coefs = c("Constant" = "(Intercept)", "Female" = "female", "Married" = "married", "Female * Married" = "female:married"), statistics = c("N" = "nobs", "R-Squared" = "r.squared", "SER" = "sigma"), number_format = 2)| (1) | |
|---|---|
| Constant | 5.17 *** |
| (0.36) | |
| Female | -0.56 |
| (0.47) | |
| Married | 2.82 *** |
| (0.44) | |
| Female * Married | -2.86 *** |
| (0.61) | |
| N | 526 |
| R-Squared | 0.18 |
| SER | 3.35 |
| *** p < 0.001; ** p < 0.01; * p < 0.05. | |
2 Dummies Interaction: Interpretting Coefficients
^wagei=5.17−0.56femalei+2.82marriedi−2.86(femalei×marriedi)
| Men | Women | |
|---|---|---|
| Unmarried | $5.17 | $4.61 |
| Married | $7.98 | $4.57 |
2 Dummies Interaction: Interpretting Coefficients
^wagei=5.17−0.56femalei+2.82marriedi−2.86(femalei×marriedi)
| Men | Women | |
|---|---|---|
| Unmarried | $5.17 | $4.61 |
| Married | $7.98 | $4.57 |
- Wage for unmarried men: ^β0=5.17
2 Dummies Interaction: Interpretting Coefficients
^wagei=5.17−0.56femalei+2.82marriedi−2.86(femalei×marriedi)
| Men | Women | |
|---|---|---|
| Unmarried | $5.17 | $4.61 |
| Married | $7.98 | $4.57 |
- Wage for unmarried men: ^β0=5.17
- Wage for married men: ^β0+^β2=5.17+2.82=7.98
2 Dummies Interaction: Interpretting Coefficients
^wagei=5.17−0.56femalei+2.82marriedi−2.86(femalei×marriedi)
| Men | Women | |
|---|---|---|
| Unmarried | $5.17 | $4.61 |
| Married | $7.98 | $4.57 |
- Wage for unmarried men: ^β0=5.17
- Wage for married men: ^β0+^β2=5.17+2.82=7.98
- Wage for unmarried women: ^β0+^β1=5.17−0.56=4.61
2 Dummies Interaction: Interpretting Coefficients
^wagei=5.17−0.56femalei+2.82marriedi−2.86(femalei×marriedi)
| Men | Women | |
|---|---|---|
| Unmarried | $5.17 | $4.61 |
| Married | $7.98 | $4.57 |
- Wage for unmarried men: ^β0=5.17
- Wage for married men: ^β0+^β2=5.17+2.82=7.98
- Wage for unmarried women: ^β0+^β1=5.17−0.56=4.61
- Wage for married women: ^β0+^β1+^β2+^β3=5.17−0.56+2.82−2.86=4.57
2 Dummies Interaction: Interpretting Coefficients
^wagei=5.17−0.56femalei+2.82marriedi−2.86(femalei×marriedi)
| Men | Women | |
|---|---|---|
| Unmarried | $5.17 | $4.61 |
| Married | $7.98 | $4.57 |
2 Dummies Interaction: Interpretting Coefficients
^wagei=5.17−0.56femalei+2.82marriedi−2.86(femalei×marriedi)
| Men | Women | |
|---|---|---|
| Unmarried | $5.17 | $4.61 |
| Married | $7.98 | $4.57 |
- ^β0: Wage for unmarried men
2 Dummies Interaction: Interpretting Coefficients
^wagei=5.17−0.56femalei+2.82marriedi−2.86(femalei×marriedi)
| Men | Women | |
|---|---|---|
| Unmarried | $5.17 | $4.61 |
| Married | $7.98 | $4.57 |
- ^β0: Wage for unmarried men
- ^β2: Effect of marriage on wages for men
2 Dummies Interaction: Interpretting Coefficients
^wagei=5.17−0.56femalei+2.82marriedi−2.86(femalei×marriedi)
| Men | Women | |
|---|---|---|
| Unmarried | $5.17 | $4.61 |
| Married | $7.98 | $4.57 |
- ^β0: Wage for unmarried men
- ^β2: Effect of marriage on wages for men
- ^β2: Difference in wages between men and women who are unmarried
2 Dummies Interaction: Interpretting Coefficients
^wagei=5.17−0.56femalei+2.82marriedi−2.86(femalei×marriedi)
| Men | Women | |
|---|---|---|
| Unmarried | $5.17 | $4.61 |
| Married | $7.98 | $4.57 |
- ^β0: Wage for unmarried men
- ^β2: Effect of marriage on wages for men
- ^β2: Difference in wages between men and women who are unmarried
- ^β3: Difference in:
- effect of Marriage on wages between men and women
- effect of Gender on wages between unmarried and married individuals
Interactions Between Two Continuous Variables
Interactions Between Two Continuous Variables

Interactions Between Two Continuous Variables

- Does the marginal effect of X1 on Y depend on what X2 is set to?
Interactions Between Two Continuous Variables
Yi=β0+β1X1i+β2X2i+β3(X1i×X2i)
Interactions Between Two Continuous Variables
Yi=β0+β1X1i+β2X2i+β3(X1i×X2i)
- To interpret coefficients, compare changes after changing ΔX1i (holding X2 constant):
Yi+ΔYi=β0+β1(X1+ΔX1i)β2X2i+β3((X1i+ΔX1i)×X2i)
Interactions Between Two Continuous Variables
Yi=β0+β1X1i+β2X2i+β3(X1i×X2i)
- To interpret coefficients, compare changes after changing ΔX1i (holding X2 constant):
Yi+ΔYi=β0+β1(X1+ΔX1i)β2X2i+β3((X1i+ΔX1i)×X2i)
- Take the difference to get:
Interactions Between Two Continuous Variables
Yi=β0+β1X1i+β2X2i+β3(X1i×X2i)
- To interpret coefficients, compare changes after changing ΔX1i (holding X2 constant):
Yi+ΔYi=β0+β1(X1+ΔX1i)β2X2i+β3((X1i+ΔX1i)×X2i)
- Take the difference to get:
ΔYi=β1ΔX1i+β3X2iΔX1iΔYiΔX1i=β1+β3X2i
Interactions Between Two Continuous Variables
Yi=β0+β1X1i+β2X2i+β3(X1i×X2i)
- To interpret coefficients, compare changes after changing ΔX1i (holding X2 constant):
Yi+ΔYi=β0+β1(X1+ΔX1i)β2X2i+β3((X1i+ΔX1i)×X2i)
- Take the difference to get:
ΔYi=β1ΔX1i+β3X2iΔX1iΔYiΔX1i=β1+β3X2i
- The effect of X1→Yi depends on X2
- β3: increment to the effect of X1→Yi for every 1 unit change in X2
Continuous Variables Interaction: Example
Example: Do education and experience interact in their determination of wages?
^wagei=^β0+^β1educi+^β2experi+^β3(educi×experi)
- Estimated effect of education on wages depends on the amount of experience (and vice versa)!
ΔwageΔeduc=^β1+β3experi
ΔwageΔexper=^β2+β3educi
- This is a type of nonlinearity (we will examine nonlinearities next lesson)
Continuous Variables Interaction: In R I
reg_cont <- lm(wage ~ educ + exper + educ:exper, data = wages)reg_cont %>% tidy()| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -2.86 | 1.18 | -2.42 | 0.0158 |
| educ | 0.602 | 0.0899 | 6.69 | 5.64e-11 |
| exper | 0.0458 | 0.0426 | 1.07 | 0.283 |
| educ:exper | 0.00206 | 0.00349 | 0.591 | 0.555 |
Continuous Variables Interaction: In R II
library(huxtable)huxreg(reg_cont, coefs = c("Constant" = "(Intercept)", "Education" = "educ", "Experience" = "exper", "Education * Experience" = "educ:exper"), statistics = c("N" = "nobs", "R-Squared" = "r.squared", "SER" = "sigma"), number_format = 3)| (1) | |
|---|---|
| Constant | -2.860 * |
| (1.181) | |
| Education | 0.602 *** |
| (0.090) | |
| Experience | 0.046 |
| (0.043) | |
| Education * Experience | 0.002 |
| (0.003) | |
| N | 526 |
| R-Squared | 0.226 |
| SER | 3.259 |
| *** p < 0.001; ** p < 0.01; * p < 0.05. | |
Continuous Variables Interaction: Marginal Effects
^wagesi=−2.860+0.602educi+0.047experi+0.002(educi×experi)
Continuous Variables Interaction: Marginal Effects
^wagesi=−2.860+0.602educi+0.047experi+0.002(educi×experi)
Marginal Effect of Education on Wages by Years of Experience:
| Experience | ΔwageΔeduc=^β1+^β3exper |
|---|---|
| 5 years | 0.602+0.002(5)=0.612 |
| 10 years | 0.602+0.002(10)=0.622 |
| 15 years | 0.602+0.002(15)=0.632 |
Continuous Variables Interaction: Marginal Effects
^wagesi=−2.860+0.602educi+0.047experi+0.002(educi×experi)
Marginal Effect of Education on Wages by Years of Experience:
| Experience | ΔwageΔeduc=^β1+^β3exper |
|---|---|
| 5 years | 0.602+0.002(5)=0.612 |
| 10 years | 0.602+0.002(10)=0.622 |
| 15 years | 0.602+0.002(15)=0.632 |
- Marginal effect of education → wages increases with more experience
Continuous Variables Interaction: Marginal Effects
^wagesi=−2.860+0.602educi+0.047experi+0.002(educi×experi)
Continuous Variables Interaction: Marginal Effects
^wagesi=−2.860+0.602educi+0.047experi+0.002(educi×experi)
Marginal Effect of Experience on Wages by Years of Education:
| Education | ΔwageΔexper=^β2+^β3educ |
|---|---|
| 5 years | 0.047+0.002(5)=0.057 |
| 10 years | 0.047+0.002(10)=0.067 |
| 15 years | 0.047+0.002(15)=0.077 |
Continuous Variables Interaction: Marginal Effects
^wagesi=−2.860+0.602educi+0.047experi+0.002(educi×experi)
Marginal Effect of Experience on Wages by Years of Education:
| Education | ΔwageΔexper=^β2+^β3educ |
|---|---|
| 5 years | 0.047+0.002(5)=0.057 |
| 10 years | 0.047+0.002(10)=0.067 |
| 15 years | 0.047+0.002(15)=0.077 |
- Marginal effect of experience → wages increases with more education
Continuous Variables Interaction: Marginal Effects
^wagesi=−2.860+0.602educi+0.047experi+0.002(educi×experi)
Marginal Effect of Experience on Wages by Years of Education:
| Education | ΔwageΔexper=^β2+^β3educ |
|---|---|
| 5 years | 0.047+0.002(5)=0.057 |
| 10 years | 0.047+0.002(10)=0.067 |
| 15 years | 0.047+0.002(15)=0.077 |
Marginal effect of experience → wages increases with more education
If you want to estimate the marginal effects more precisely, and graph them, see the appendix in today’s class page