3.7 — Regression with Interaction Effects — Class Notes

Overview
Readings
Slides
Practice Problems
Live Class Session on Zoom
Appendix: Marginal Effects for Two-Continuous Variable Interactions
- Standard Error of Marginal Effects

Thursday, October 29, 2020

Overview

Today we continue examining how to use categorical data in regression, particularly focusing on interactions between variables. We look at three types of interaction effects: 1. Interaction between a continuous variable & a dummy variable 2. Interaction between two dummy variables 3. Interaction between two continuous variables

We will also be working on practice problems today in R.

Readings

See today’s suggested readings.

Slides

Practice Problems

Today we will be working on practice problems. Answers will be posted on that page later.

Live Class Session on Zoom

The live class Zoom meeting link can be found on Blackboard (see LIVE ZOOM MEETINGS on the left navigation menu), starting at 11:30 AM.

If you are unable to join today’s live session, or if you want to review, you can find the recording stored on Blackboard via Panopto (see Class Recordings on the left navigation menu).

Appendix: Marginal Effects for Two-Continuous Variable Interactions

In class, we looked at the effects of education on wages, experience on wages, and the interaction between education and experience on wages:

\[\widehat{wage_i}=\hat{\beta_0}+\hat{\beta_1} \, education_i+\hat{\beta_2} \, experience_i+\hat{\beta_3}(education_i \times experience_i)\]

Using the wage1 data in the wooldridge package, we found the following:

library(tidyverse)
library(broom)
wages<-wooldridge::wage1
reg_cont <- lm(wage ~ educ + exper + educ:exper, data = wages)
reg_cont %>% tidy()

## # A tibble: 4 x 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept) -2.86      1.18       -2.42  1.58e- 2
## 2 educ         0.602     0.0899      6.69  5.64e-11
## 3 exper        0.0458    0.0426      1.07  2.83e- 1
## 4 educ:exper   0.00206   0.00349     0.591 5.55e- 1

Let’s extract and save each of these \(\hat{\beta}\)’s for later use.

b_1 <- reg_cont %>%
  tidy() %>%
  filter(term == "educ") %>%
  pull(estimate)

b_2 <- reg_cont %>%
  tidy() %>%
  filter(term == "exper") %>%
  pull(estimate)

b_3 <- reg_cont %>%
  tidy() %>%
  filter(term == "educ:exper") %>%
  pull(estimate)

# let's check each of these
b_1

## [1] 0.6017355

b_2

## [1] 0.04576891

b_3

## [1] 0.002062345

We know that the marginal effect of each of the two \(X\) variables on \(Y\) depends on the value of the other \(X\) variable:

Variable	Marginal Effect on Wages (Formula)	Marginal Effect on Wages (Estimate)
Education	\(\hat{\beta_1}+\hat{\beta_3} \, Experience_i\)	0.6037978 \(\, Experience_i\)
Experience	\(\hat{\beta_2}+\hat{\beta_3} \, Education_i\)	0.6037978 \(\, Education_i\)

We can get the marginal effects more precisely by making a function of each marginal effect, using the coefficients saved above. To make a your own function in R (a very handy thing to do!), simply define an object as my_function<- function(){}. Inside the () goes any arguments the function will need (here, it’s the value of the other variable), and then the formula to apply to that argument. Then you can run the function on any object.

As a simple example, to make a function that squares x:

# make function called "square" that squares x
square<-function(x){x^2}

# test it on the value 4
square(4)

## [1] 16

# test it on all of these values
square(1:4)

## [1]  1  4  9 16

Now let’s make a function for the marginal effect of education (by experience):

# make marginal effect of education on wages by years of experience function
# input is years of experience
me_educ<-function(exper){b_1*b_3*exper}

# now its a function, let's input 5 years, 10 years, 15 years of experience
me_educ(c(5,10,15))

## [1] 0.006204929 0.012409858 0.018614788

Now let’s make a function for the marginal effect of experience (by education):

# make marginal effect of experience on wages by years of education function
# input is years of education
me_exper<-function(educ){b_2*b_3*educ}

# now its a function, let's input 5 years, 10 years, 15 years of education
me_exper(c(5,10,15))

## [1] 0.0004719563 0.0009439126 0.0014158689

We can now graph these

margin_educ<-ggplot(data = wages)+
  aes(x = exper)+
  stat_function(fun = me_educ, geom = "line", color = "blue")+
  scale_y_continuous(labels = scales::dollar)+
  labs(x = "Years of Experience",
       y = "Marginal Effect of Education on Wages",
       title = "Effect of Education on Wages, by Years of Experience")+
  ggthemes::theme_pander(base_family = "Fira Sans Condensed", base_size = 14)
margin_educ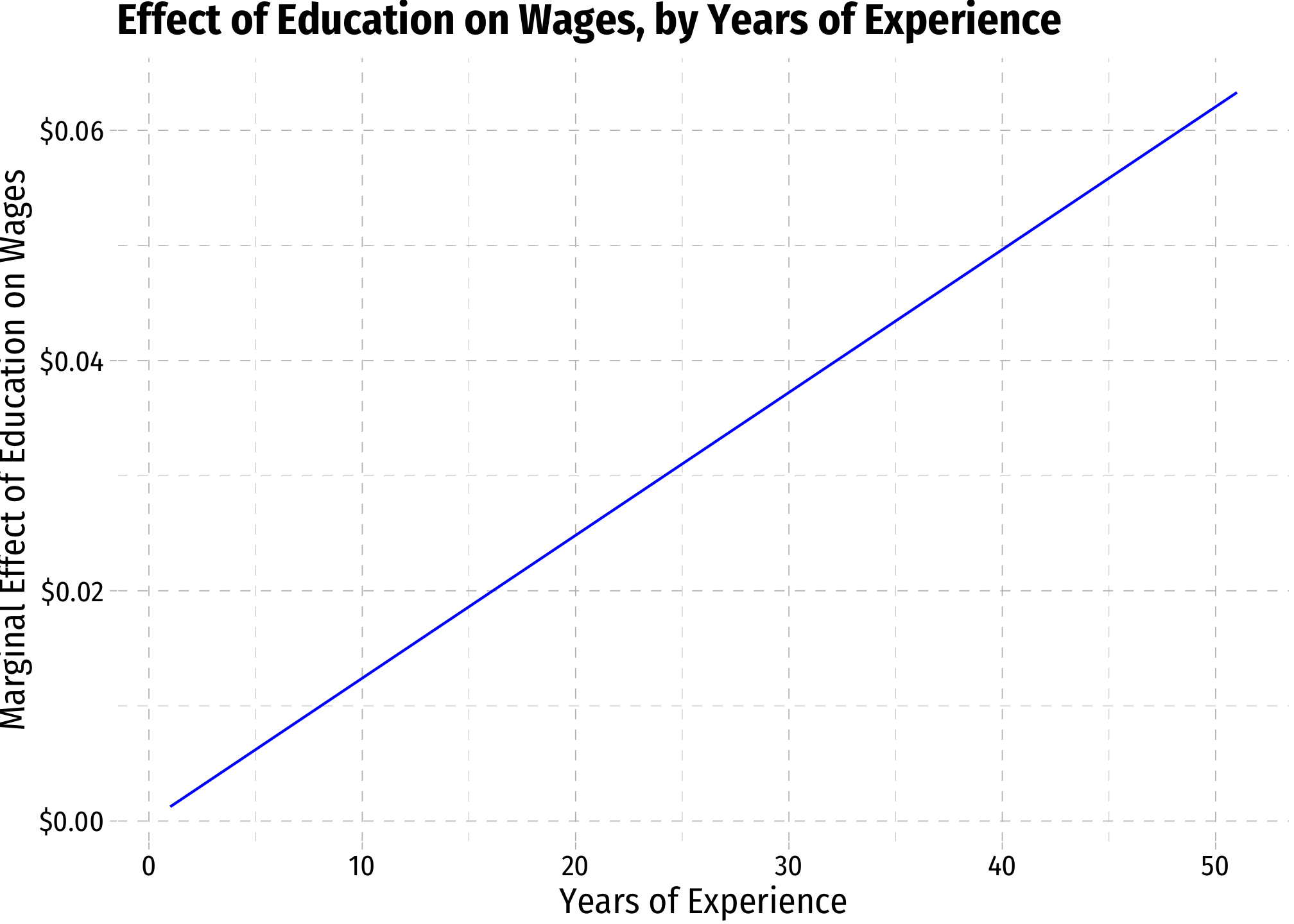

margin_exper<-ggplot(data = wages)+
  aes(x = educ)+
  stat_function(fun = me_exper, geom = "line", color = "blue")+
  scale_y_continuous(labels = function(x){paste0("$",x)})+
  labs(x = "Years of Education",
       y = "Marginal Effect of Experience on Wages",
       title = "Effect of Experience on Wages, by Years of Education")+
  ggthemes::theme_pander(base_family = "Fira Sans Condensed", base_size = 14)
margin_exper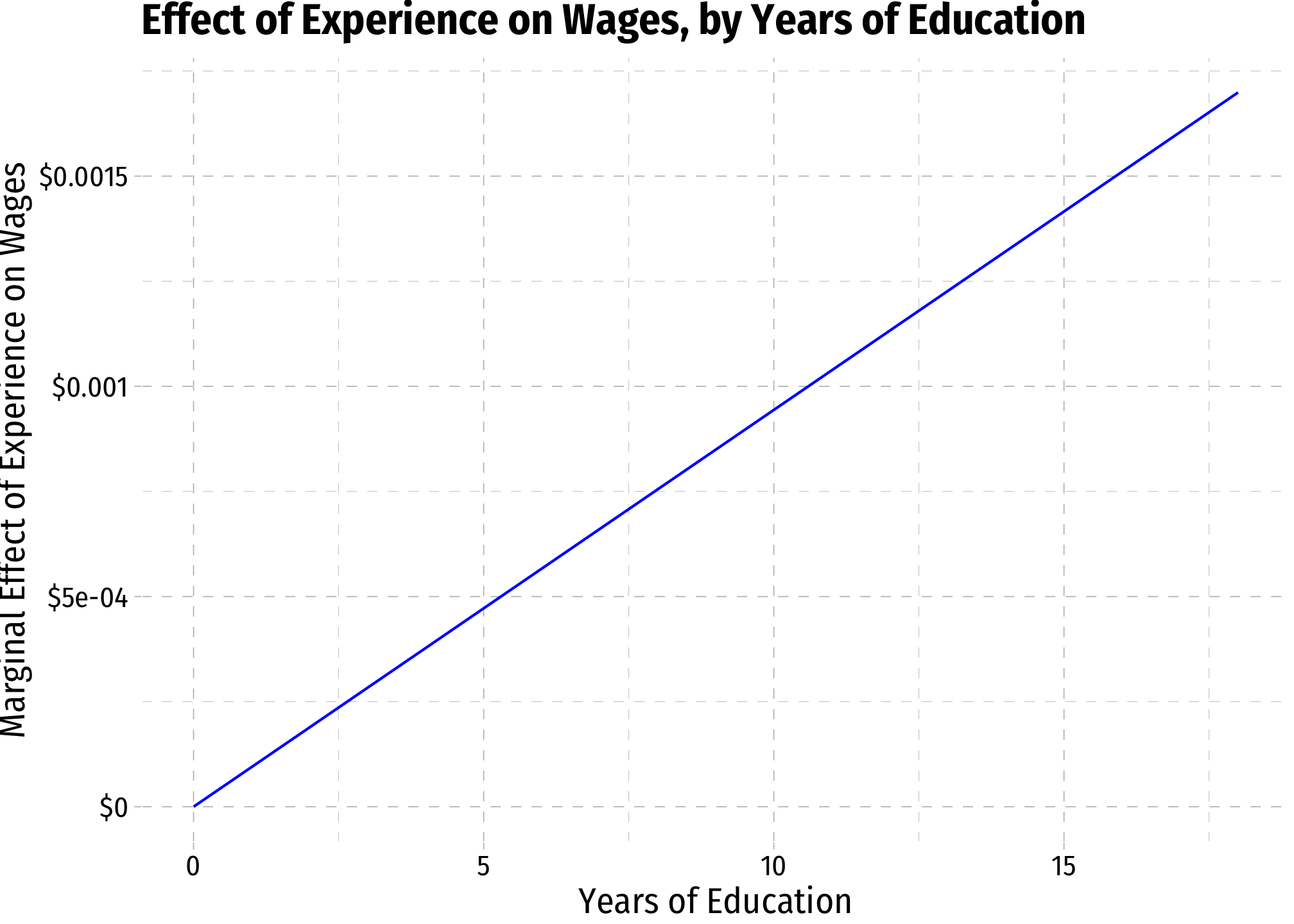

Standard Error of Marginal Effects

If we want to add the standard error to these graphs, we need to extract the \(se(\hat{\beta})\)’s from the original regression output:

se_b_1 <- reg_cont %>%
  tidy() %>%
  filter(term == "educ") %>%
  pull(std.error)

se_b_2 <- reg_cont %>%
  tidy() %>%
  filter(term == "exper") %>%
  pull(std.error)

se_b_3 <- reg_cont %>%
  tidy() %>%
  filter(term == "educ:exper") %>%
  pull(std.error)

# let's check each of these
se_b_1

## [1] 0.08989998

se_b_2

## [1] 0.04261376

se_b_3

## [1] 0.003490614

Now the standard error of the marginal effect is a bit tricky. The marginal effect, for example, of Education on Wages, we saw was \(\frac{\Delta Wage_i}{\Delta Education_i} = \hat{\beta_1}+\hat{\beta_3} \, Experience_i\). One property of variances (or, when square rooted, standard errors) of random variables is that:

\[var(X+aY)=var(X)+var(Y)c^2+2 \, a \, cov(X,Y)\]

Here, the \(\hat{\beta}\)’s are random variables, and \(Experience_i\) is a constant (some number, like \(a)\). So the variance is:

\[var(\hat{\beta_1}+\hat{\beta_3}Experience_i)=var(\hat{\beta_1})+var(\hat{\beta_3})Experience_i^2+2 \, Experience_i \, cov(\hat{\beta_1},\hat{\beta_3})\]

The standard error then is the square root of this. To get the covariance of \(\hat{\beta_1}\) and \(\hat{\beta_3}\), we need to extract it from something called the variance-covariance matrix. A regression creates and stores a matrix that contains the covariances of all \(\hat{\beta}\)’s with each other (and the covariance of any \(\hat{\beta}\) with itself is the variance of that \(\hat{\beta})\):

# look at variance-covariance matrix
vcov(reg_cont)

##              (Intercept)          educ         exper    educ:exper
## (Intercept)  1.394949133 -0.1040894353 -0.0412570602  3.134939e-03
## educ        -0.104089435  0.0080820059  0.0031414567 -2.513073e-04
## exper       -0.041257060  0.0031414567  0.0018159324 -1.437215e-04
## educ:exper   0.003134939 -0.0002513073 -0.0001437215  1.218438e-05

# make it a tibble to work with using tidyverse methods
v<-as_tibble(vcov(reg_cont))

# we want the covariance between beta 1 and beta 3, save as "cov_b1_b3"
cov_b1_b3<-v %>%
  slice(2) %>%
  pull(`educ:exper`) 
cov_b1_b3 # look at it

## [1] -0.0002513073

# lets also get the covariance between beta 2 and beta 3 (for later)

cov_b2_b3<-v %>%
  slice(3) %>%
  pull(`educ:exper`)
cov_b2_b3

## [1] -0.0001437215

# make a function of the variance of the marginal effect of education on wages
var_me_educ=function(experience){(se_b_1)^2+(se_b_3)^2*experience+2*experience*cov_b1_b3}

# now square root it to get standard error
se_me_educ=function(experience){sqrt(var_me_educ(experience))}

# to plot a 95% confidence interval of the marginal effect, lets make upper and lower CI values as a function of experience
CI_me_educ_upper=function(experience){me_educ(experience)+1.96*se_me_educ(experience)}
CI_me_educ_lower=function(experience){me_educ(experience)-1.96*se_me_educ(experience)}

# lets now add these into the data
wages2<-wages %>%
  select(exper) %>%
  mutate(me_educ = me_educ(exper),
         CI_educ_lower = CI_me_educ_lower(exper),
         CI_educ_upper = CI_me_educ_upper(exper)
         )

## Warning: Problem with `mutate()` input `CI_educ_lower`.
## ℹ NaNs produced
## ℹ Input `CI_educ_lower` is `CI_me_educ_lower(exper)`.

## Warning in sqrt(var_me_educ(experience)): NaNs produced

## Warning: Problem with `mutate()` input `CI_educ_upper`.
## ℹ NaNs produced
## ℹ Input `CI_educ_upper` is `CI_me_educ_upper(exper)`.

## Warning in sqrt(var_me_educ(experience)): NaNs produced

# and graph it!
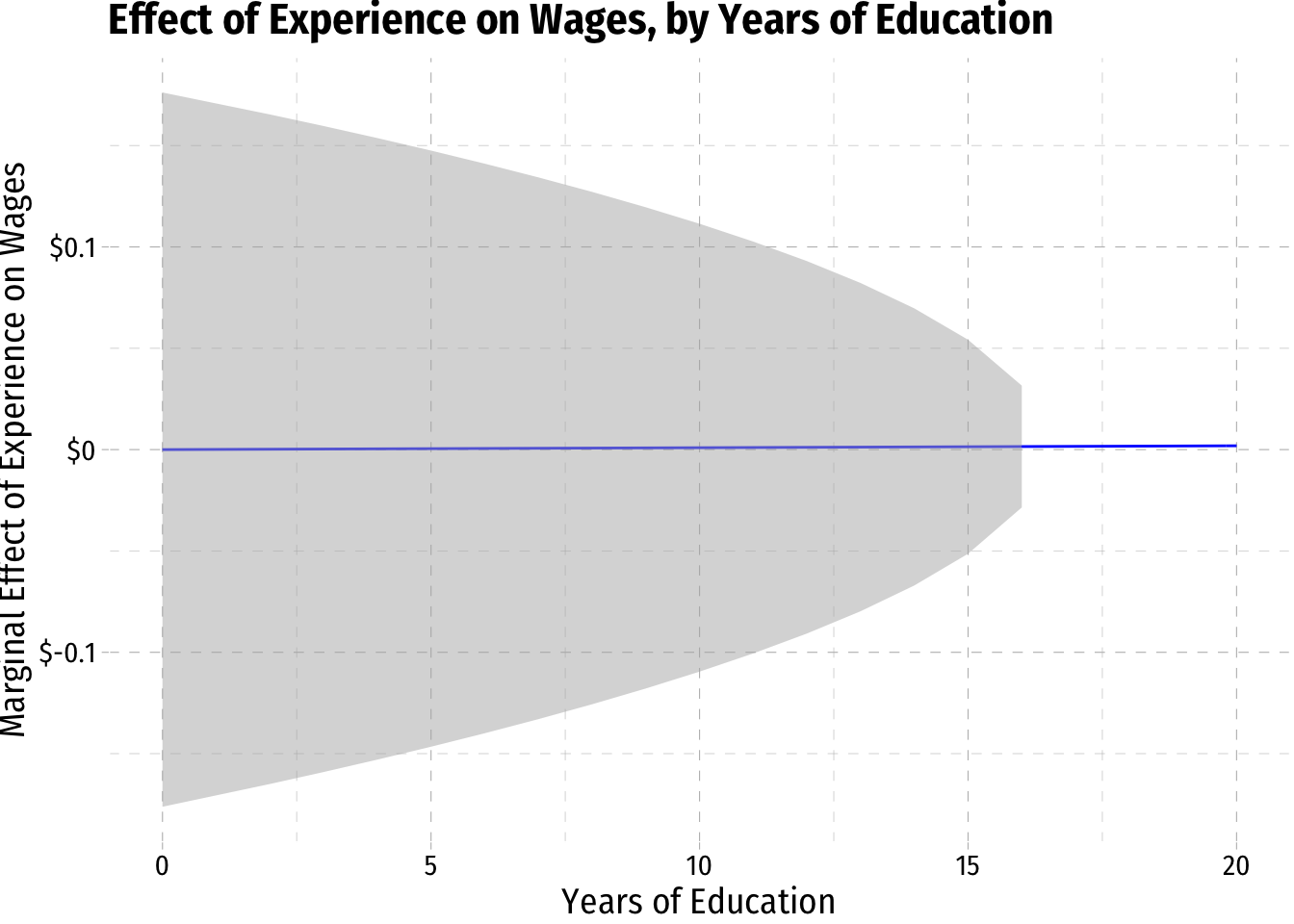
margin_educ+
  geom_ribbon(data = wages2, aes(ymin=CI_educ_lower, ymax=CI_educ_upper), fill = "grey70", alpha = 0.5)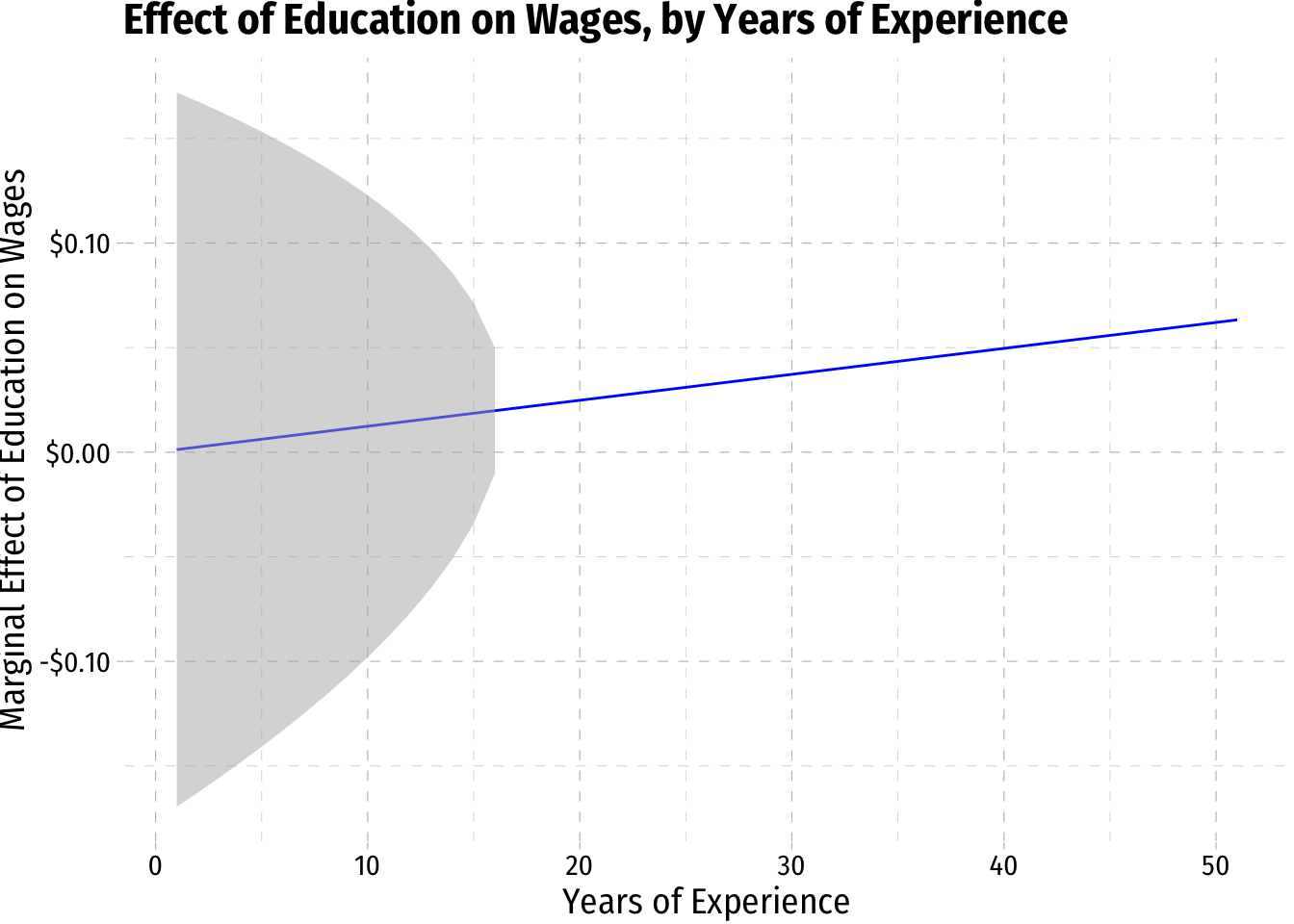

# do the same for the marginal effect of experience on wages
var_me_exper=function(education){(se_b_2)^2+(se_b_3)^2*education+2*education*cov_b2_b3}

# now square root it to get standard error
se_me_exper=function(education){sqrt(var_me_educ(education))}

# to plot a 95% confidence interval of the marginal effect, lets make upper and lower CI values as a function of experience
CI_me_exper_upper=function(education){me_exper(education)+1.96*se_me_exper(education)}
CI_me_exper_lower=function(education){me_exper(education)-1.96*se_me_exper(education)}

# lets now add these into the data
wages3<-wages %>%
  select(educ) %>%
  mutate(me_exper = me_exper(educ),
         CI_exper_lower = CI_me_exper_lower(educ),
         CI_exper_upper = CI_me_exper_upper(educ)
         )

## Warning: Problem with `mutate()` input `CI_exper_lower`.
## ℹ NaNs produced
## ℹ Input `CI_exper_lower` is `CI_me_exper_lower(educ)`.

## Warning in sqrt(var_me_educ(education)): NaNs produced

## Warning: Problem with `mutate()` input `CI_exper_upper`.
## ℹ NaNs produced
## ℹ Input `CI_exper_upper` is `CI_me_exper_upper(educ)`.

## Warning in sqrt(var_me_educ(education)): NaNs produced

# and graph it!
margin_exper+
  geom_ribbon(data = wages3, aes(ymin=CI_exper_lower, ymax=CI_exper_upper), fill = "grey70", alpha = 0.5)+
  scale_x_continuous(limits=c(0,20))